How to Play Sudoku
The goal of Sudoku is to fill each row, column, and 3x3 block with the numbers 1 through 9, ensuring that no number is repeated within any row, column, or block.
While Sudoku is a number game, no math is required. It is a logic puzzle that challenges you to use reasoning and deduction to place numbers correctly—each puzzle has only one right answer.
We have thousands of free Sudoku puzzles and Sudoku printables to download and enjoy anywhere.
Rules

Each Sudoku grid has 81 cells arranged in a 9x9 layout and subdivided into nine 3x3 blocks. At the start of each game, some of the cells will be filled with numbers that allow you to figure out the placement of numbers in blank cells.
The more cells that are filled, the easier it is to solve the puzzle. As you increase the difficulty level, fewer cells will be filled out, and you’ll need to use more advanced strategies to problem solve.
No matter the skill level, every Sudoku game will follow these rules:
- Use numbers 1 through 9 once in each row, column, and 3x3 block.
- You cannot repeat numbers in a row, column, or 3x3 block. If there are duplicates, the solution is incorrect.
Each Sudoku puzzle has only one right answer, and solving it requires careful observation and patience.
Gameplay and Features
Our online Sudoku offers multiple customizations so that you can set up the game based on your preferences.
To fill out the grid, choose a number and then click on the cell you’d like to fill in. If you pressed the wrong number or changed your mind, use the Undo button.
Other buttons and features can help you further gameplay:
- This Number is a Possibility: Check this box to add small, superscript numbers to a cell, representing potential options for that spot. These notes act as reminders of which numbers could fit, helping you eliminate incorrect choices and narrow down your options.
- Check Moves: At any point in the game, you can click the Check Moves button to verify that your answers are correct. Any incorrect answers will be highlighted in red.
- Show Solution: If you get stuck or can’t solve the puzzle, use this option to automatically fill in the correct answers.
- Reset: This clears the grid of all your entries, returning the puzzle to its original state.
- Reset Poss: This clears the grid of the notes of possible answers you’ve added.
You can further customize your game by checking or unchecking the options below the buttons.
Difficulty Levels
We have five difficulty levels: Easy, Medium, Hard, Expert, and Evil. As each level progresses, you are given fewer numbers at the onset of the game, making the puzzles increasingly complex. Additionally, we offer Sudoku for Kids, which has 4x4 and 6x6 grid options and 16x16 Sudoku that includes both letters and numbers for a different kind of challenge.
Sudoku Strategies
While Sudoku rules are simple, solving the 9x9 grid isn’t always easy. These tips and strategies will help you master the game.
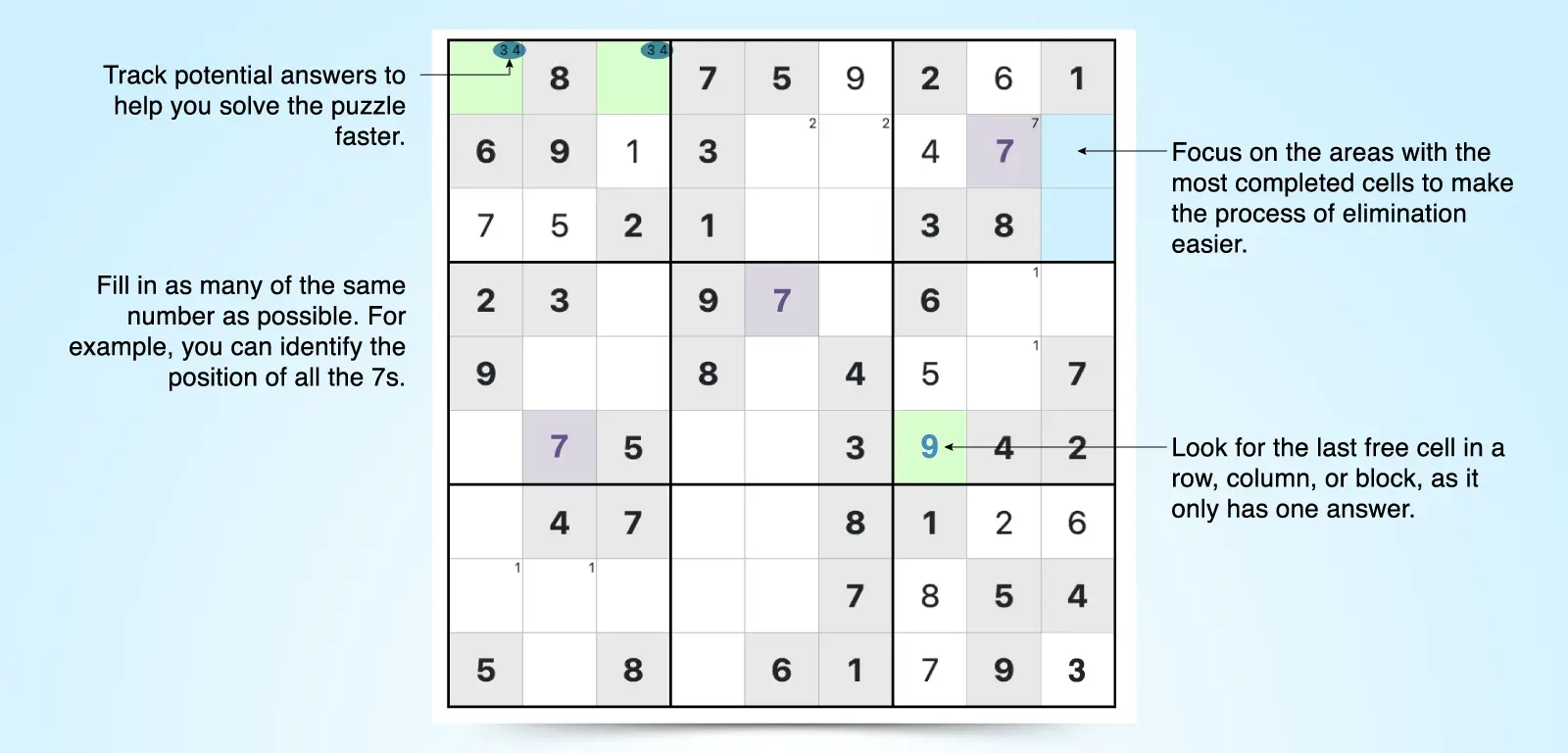
- Start with rows, columns, and 3x3 blocks that have the most filled cells. The fewer cells left to fill, the easier the process of elimination is. This will help you get some quick wins, allowing you to build momentum and tackle the more challenging sections.
- Track possibilities. Use the Possibilities feature to note multiple potential options in each cell. Update your notes as you remove possibilities, helping you to solve the puzzle faster.
- Focus on one number at a time. Choose a number and try to place it as many times as possible on the grid, then move on to the next number.
- Look for the last free cell in a row, column, or 3x3 block. If there is only one cell left, there is only one possible number that can go there.
- Evaluate the row, column, and 3x3 block that intersect a specific empty cell. The numbers present in the same row, column, and block the cell belongs to cannot be the answer for that cell. Reviewing all three helps give you a bigger picture view. This is called the last possible number strategy.
- Use elimination techniques. More advanced levels require careful note taking and rely on the process of elimination. Strategies like naked pairs, X-wing, and Y-wing will help you narrow down your options.
With these rules, features, and strategies in mind, you’re ready to dive in! Whether you’re a beginner or strategy pro, play Sudoku online for free and challenge yourself with daily puzzles.