Y-Wing Sudoku Technique: How to Find and Examples
Used as a candidate eliminator, the Y-wing strategy is similar to the X-wing technique, but it uses three cells instead of four. It can help you find answers in other cells or cause a chain reaction of elimination to further narrow possible candidates.
Whether you've just begun exploring Sudoku strategies or are an advanced solver, the Y-wing Sudoku technique is suitable for difficulty levels from intermediate on up. If you want to master this technique, our guide offers examples and step-by-step instructions for finding Y-wing patterns and applying the strategy when you play Sudoku.
Simplifying the Y-Wing Technique
To find a Y-wing, you look for three bi-value cells (cells with just two candidates) that form a two-step if-then chain (if one candidate is the answer for a cell then the other candidate must be an answer to another cell). To form this chain, the three bi-value cells must share two candidates from a group of three common candidates.
If you're familiar with the X-wing technique, you may assume the name for this strategy refers to creating a Y shape when connecting the cells, but it doesn't always look like the letter. The name refers to candidates in the three bi-value cells, like how letters are assigned to unknowns in algebra, and the x and y each stand for a different candidate. That's why the technique is also referred to as the xy-wing.
If you know the following Sudoku terminology, you can put the relationship between these three cells together and understand how they create the Y-wing pattern:
- Pivot cell: One bi-value cell has candidates x and y. It also shares a unit with two other bi-value cells that don't share a unit with each other, called pincer cells. For example, cell C1 only has two candidates, x and y.
- Pincer cell 1: One bi-value cell has candidates x and z, sharing one candidate (x) and as well as one unit with the pivot cell. For example, F1 has an x and shares the same row (1) as C1.
- Pincer cell 2: Another bi-value cell has candidates y and z, sharing one candidate (y) as well as one unit with the pivot cell, but it doesn't share a unit with the other pincer cell. For example, B2 has a y candidate and shares the same 3x3 block as C1, but it doesn't share a unit with F1.
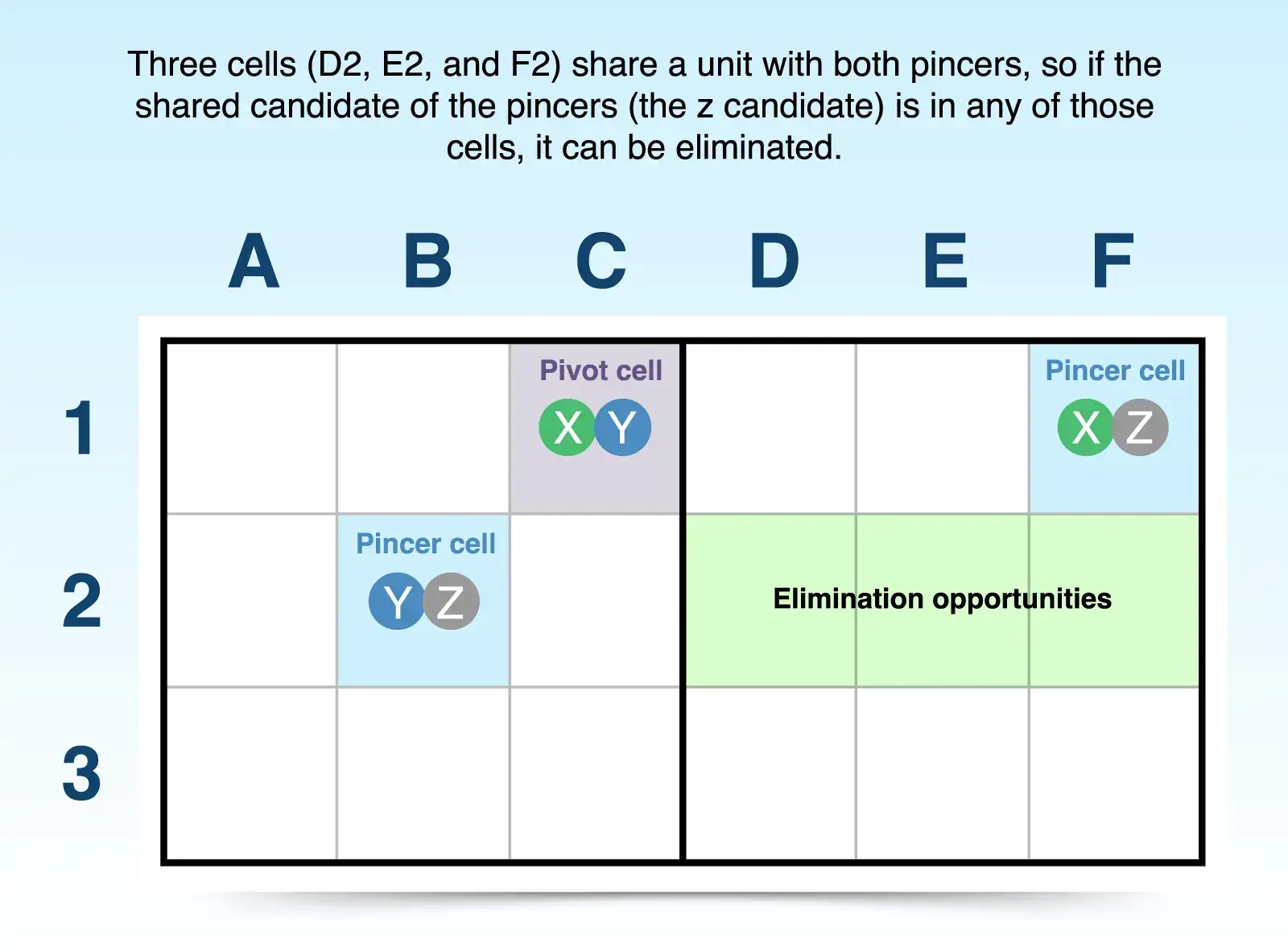
One key to the Y-wing concept is the third candidate (z), which is shared between the pincer cells. For example, candidate z is shared between B2 and F1. The x and y establish the relationship between the pivot cell and the pincers, but the third candidate ties the two pincers together.
From these relationships you have two-step if-then chain that helps you eliminate candidates:
- If C1 is x, then F1 must be z.
- If C1 is y, then B2 must be z.
So either B2 or F1 must have an answer of z. Because that answer is locked into one of those two candidates, then any cell that shares a unit (row, column, 3x3 block) with both of the pincers cannot logically have an answer of z. Thus, you can eliminate z from any of those cells.
For example, cells D2, E2, and F2 share a unit with B2 (row 2) and a unit with F1 (the same 3x3 block). So those three cells cannot logically have z as answer, which means you can eliminate that candidate from those cells.
How to Find a Sudoku Y-Wing
Advanced strategies like the Y-wing are easy to find and use if you just follow these simple steps:
- Find the pivot cell. The pivot cell is the bi-value cell with candidates xy. It also shares a unit with two other bi-value cells that don't share a unit with each other. For example, C1 is a bi-value cell that can "see" (shares a unit with) the bi-value cell in F1 because they share a row, but it also sees a bi-value cell in a separate unit, the cell B3 in the same 3x3 block as C1.
- Confirm the pincer cells. The pincer cells have two candidates. They share one candidate each with the pivot cell and the pincers cells' second candidate is a common candidate. So one has candidates xz and one has yz. For example, C1 shares a 4 candidate with B3 and a 7 candidate with F1, and B3 and F1 both have a 1 candidate. So B3 and F1 are pincer cells for C1.
- Find the candidate to be eliminated. Because of the relationship between the three cells, you can eliminate the shared candidate between the pincers in any cell those two pincers cells both see. The pivot cell proves that the candidate shared only with the pincers must be an answer in one of the pincers. For example:
- If C1 is 4 then B3 is 1.
- If C1 is 7, then F1 is 1.
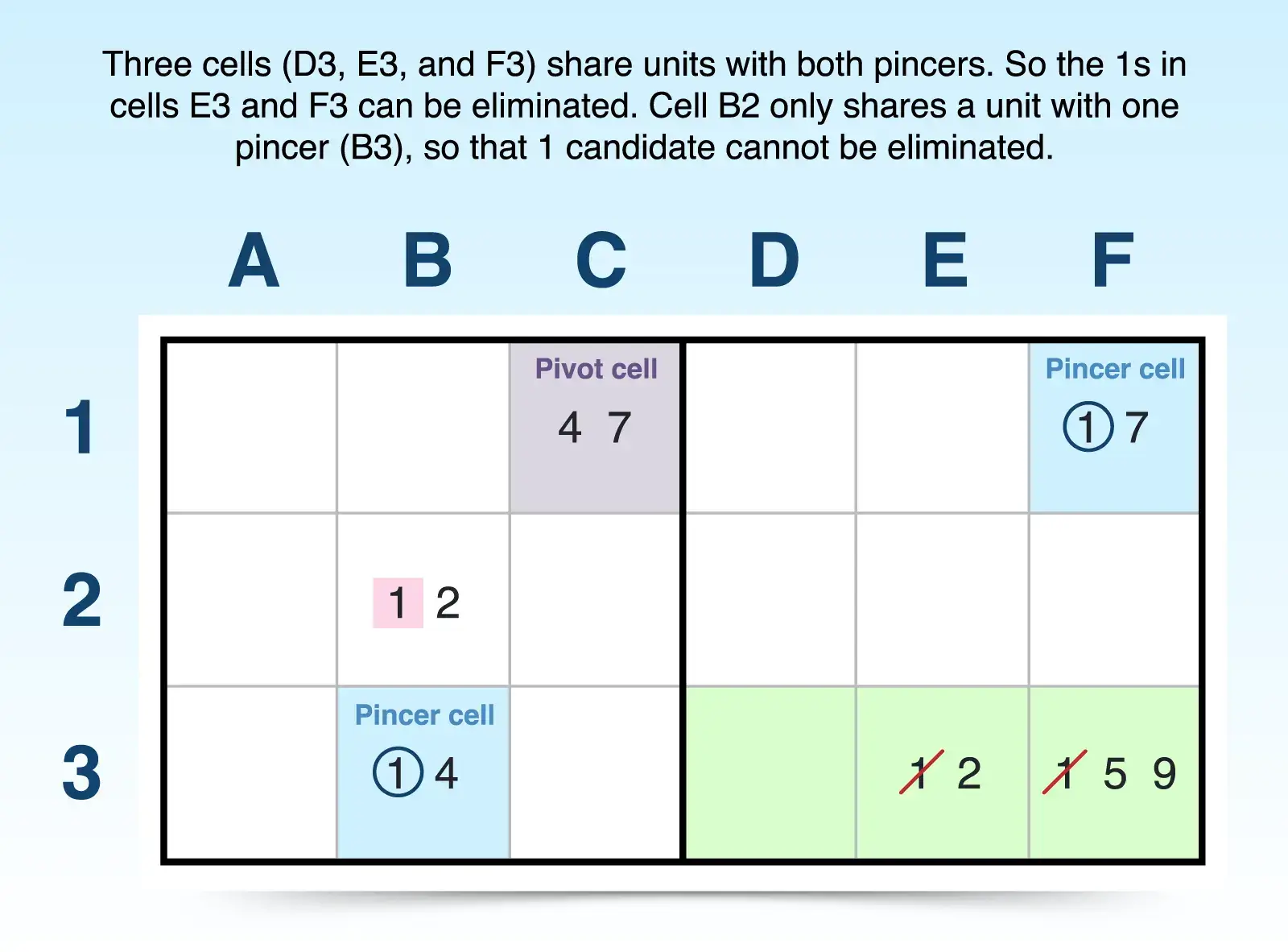
So, 1 has to be an answer in B3 or F1, and any 1 candidate in any cell those two pincers can both see, can be eliminated. For example, the 1 candidate in E3 can be eliminated because it shares the same row as B3 and the same 3x3 block as F1, and the 1 candidate in F3 can be eliminated because it shares the same row as B3 and the same column as F1. However, the 1 candidate in B2 cannot be eliminated because it shares a unit B3 but not with F1.
You won't find Y-wings in every puzzle, but any bi-value cells that aren't naked pairs could be Y-wing cells. So check to see if they have shared candidates to create the pattern.
Note that you may find a Y-wing but not be able to eliminate candidates. If this happens, don't worry - you haven't wasted your time. The more you identify them, the easier the process will be, which can lead to a big payoff that unlocks a puzzle you're stuck on.
Y-Wing Examples
When using this technique, you'll quickly discover that the closer the three cells of the Y-wing are together, the more cells both pincer candidates will see. This means you can possibly eliminate more candidates than when the cells are farther apart. These examples of Y-wings will help you understand how proximity impacts the number of candidates you can eliminate.
Y-Wing in Close Proximity
Y-wings are easier to spot when they are close together, like this one, plus they typically offer more shared cells in which candidates to be eliminated. Consider this example:
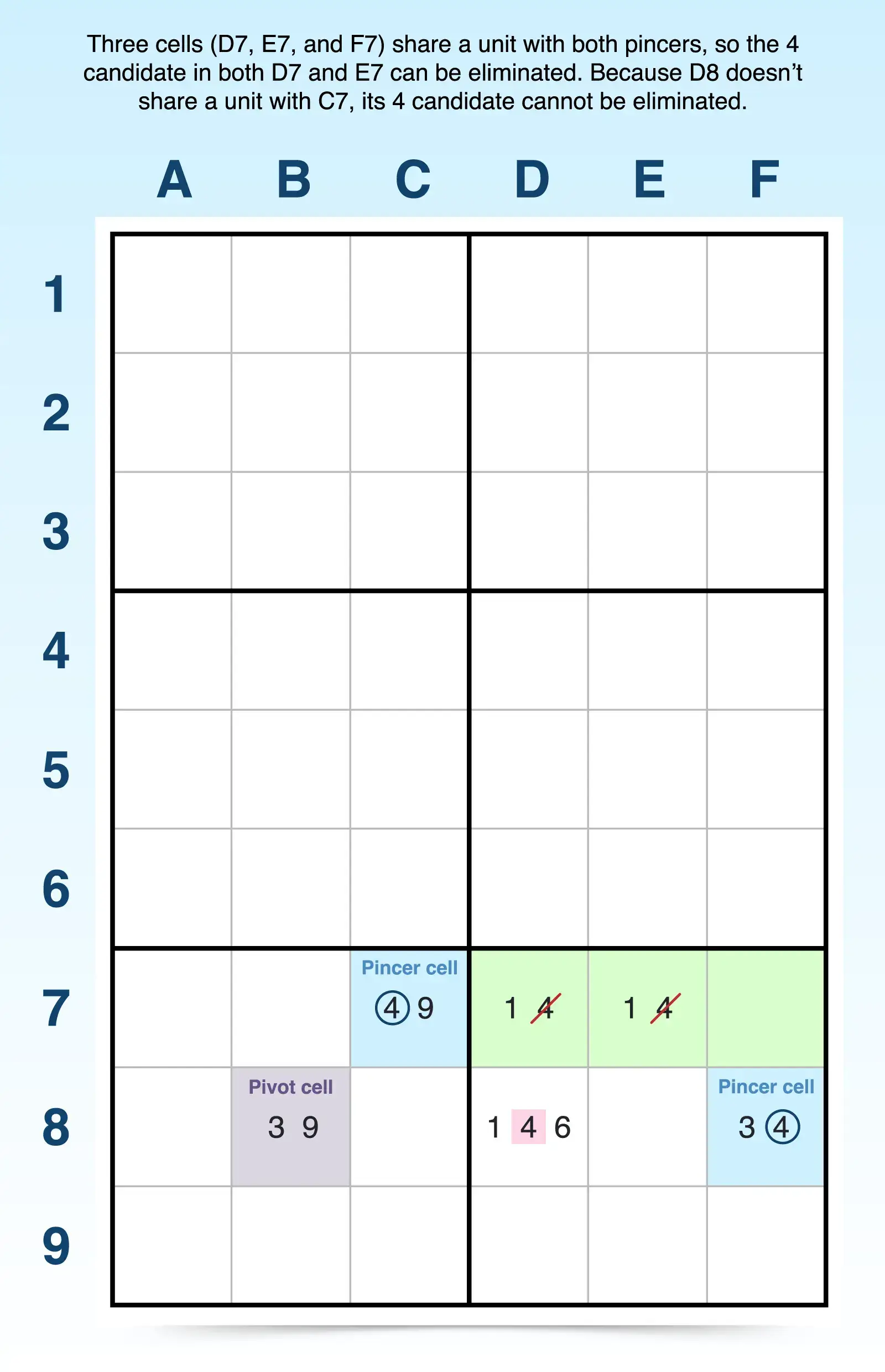
- Pivot cell: Cell B8 contains just two candidates (3, 9), and it shares one candidate each with C7 (9) and F8 (3). It also shares a unit with C7 (3x3 block) and a separate unit with F8 (row 8).
- Pincer cell 1: Cell C7 has just two candidates (4, 9). One candidate (9) is shared with the pivot cell (F8), and one candidate (4) with the other pincer cell (F8). Cell C7 shares a unit (3x3 block) with the pivot cell, B8, but it doesn't share a unit with F8.
- Pincer cell 2: Cell F8 has just two candidates (3, 4). One candidate (3) is shared with the pivot cell (F8), and one candidate (4) with the other pincer cell (C7). F8 shares a unit (row 8) with the pivot cell, B8, but it doesn't share a unit with C7, the other pincer cell.
- Elimination possibilities: The three highlighted cells in row 7 (D7, E7, and F7) show how many cells that both pincers see. If any of those cells have the candidate 4 (shared by pincer cells), that candidate can be eliminated. So cells D7 and E7 can have their 4s deleted, but not D8. Cell D8 cannot have the 4 eliminated because while it does share a unit with one pincer cell (same 3x3 as F8), it doesn't share a unit with C7.
Y-Wing Spread Farther Apart
This example shows you how your possibilities for elimination dwindle if the Y-wing is spread across a larger portion of the puzzle. Consider this example:
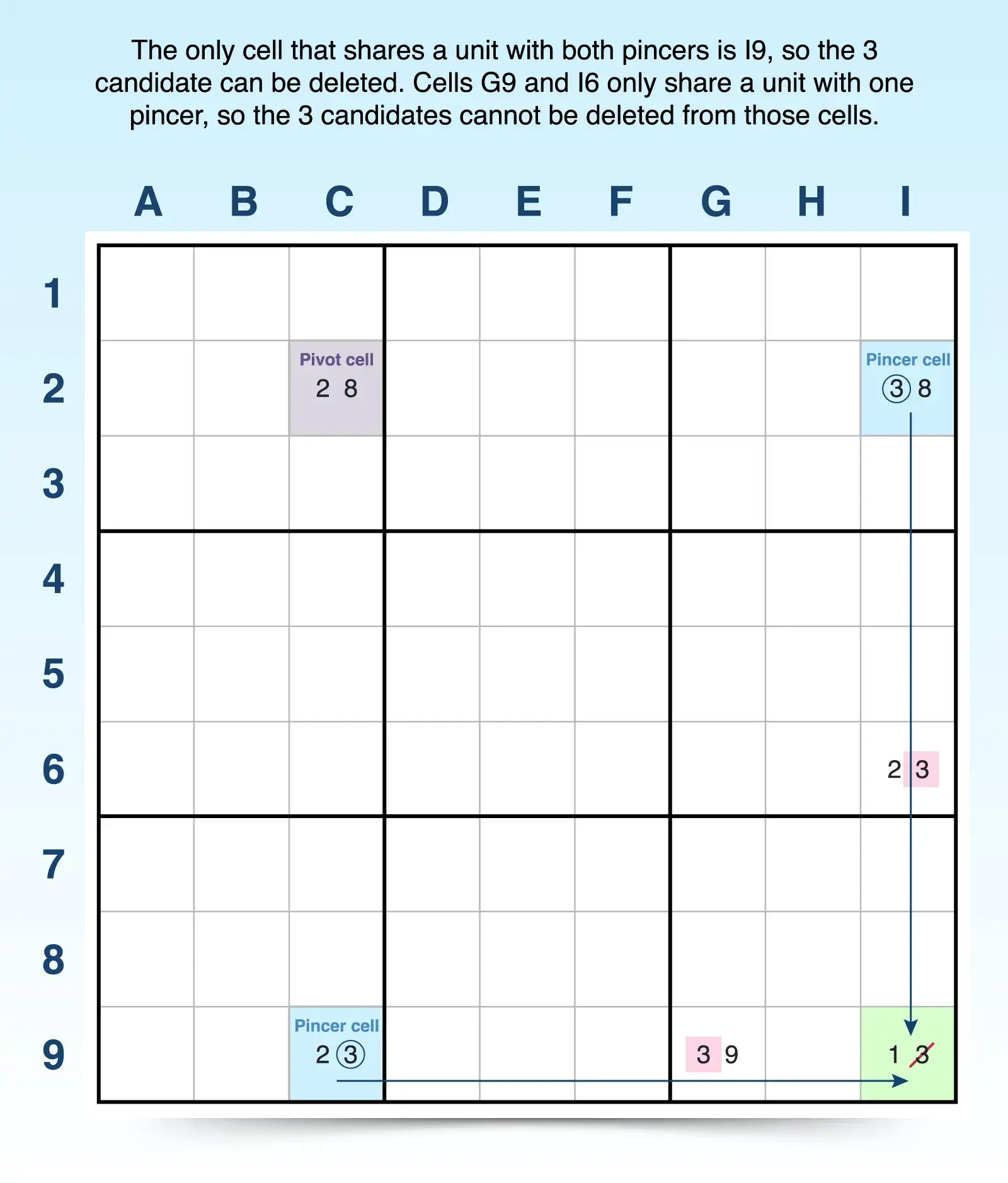
- Pivot cell: Cell C2 contains just two candidates (2, 8), and it shares one candidate each with I2 (8) and C9 (2). It also shares a unit with I2 (row 2) and a separate unit with C9 (column 9).
- Pincer cell 1: Cell I2 has just two candidates (3, 8). One candidate (8) is shared with the pivot cell (C2), and one candidate (3) with the pincer cell C9. Cell I2 shares a unit (row 2) with the pivot cell, C2, but it doesn't share a unit with C9.
- Pincer cell 2: Cell C9 has just two candidates (2, 3). One candidate (2) is shared with the pivot cell (C2), and one candidate (3) with the pincer cell I2. Cell C9 shares a unit (column C) with the pivot cell, C2, but it doesn't share a unit with I2, the other pincer cell.
- Elimination possibilities: The one highlighted cell (I9) is the only cell that both pincers can see - it shares a column with I2 and a row with C9. Because that cell has a 3 (the candidate shared by the pincer cells), that candidate can be eliminated. Although cells G9 and I6 each have a 3 candidate, it cannot be eliminated from those cells because G9 only shares a unit (row 9) with one pincer cell (C9), and I6 shares a unit (column I) with just one pincer cell (I9).
Although Sudoku puzzles become harder as you progress in difficulty levels, using strategies and techniques helps you solve them efficiently and effectively. So use this Y-wing technique in our intermediate, hard, and expert puzzles, and if you're looking for more practice, you can explore our archive for even more Sudoku puzzles to solve.