Sudoku Unique Rectangles: 5 Types and Examples

A Sudoku unique rectangle is a pattern that occurs when two candidates appear in two columns and two rows within just two blocks, creating the corners of a rectangle and resulting in two possible solutions if left unresolved. This violates the uniqueness rule in Sudoku, and you must find a way to break the pattern so that there is only one solution.

Unique rectangles (UR) are divided into several different types, from the most basic to more complex patterns, so you can find unique rectangles in puzzles at all difficulty levels, from easy Sudoku to the more difficult expert and evil puzzles. Finding one and breaking the pattern helps you eliminate candidates or find answers to specific cells, depending on the type you've found.

Use the tips in this post to find different types of unique rectangles and solve more puzzles when you play Sudoku.

How to Find Unique Rectangles

To find a unique rectangle, follow these steps:

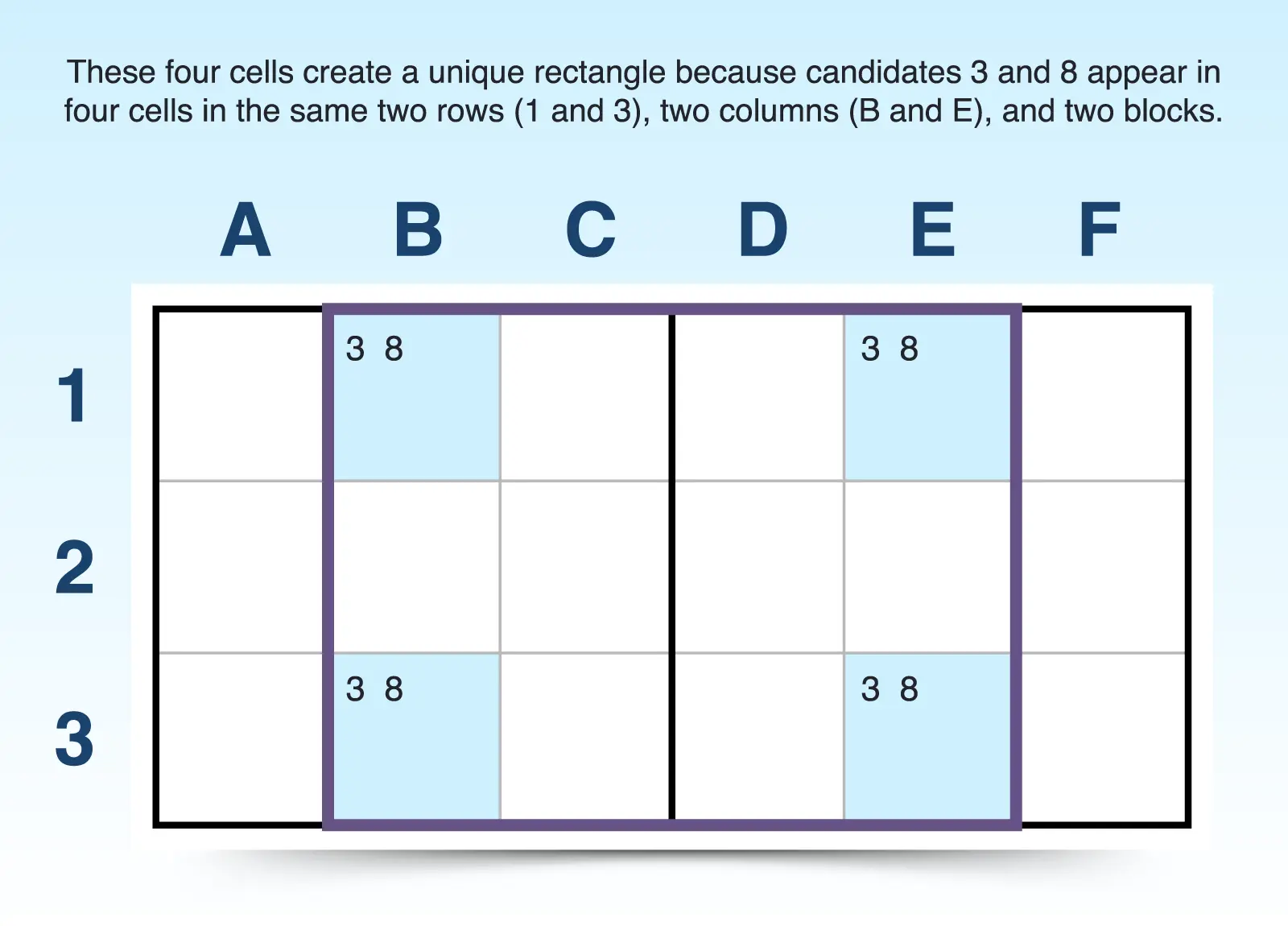
1. Find a matching pair of candidates in two cells within the same column or row. These don't need to be the only candidates in the cells, and they don't need to be limited to those two cells like in naked pairs. For example, cells B1 and B3 both contain candidates 3 and 8 in column B.
2. Find the same pair in another row or column. If your first pair is in the same row, look for another pair in a different row, but in the same columns. If they're in the same column, look in another column, but the same rows. These four cells will form the four corners of a rectangle. For example, cells E1 and E3 also contain 3 and 8, matching the rows of B1 and B3.
3. Make sure the four cells are housed in just two 3x3 blocks. The cells in a unique rectangle can only appear in two 3x3 blocks. So check to see that the cells follow this rule. For example, cells B1 and B3 are in one 3x3 block, and E1 and E3 are in a second 3x3 block.

These four cells form a unique rectangle, a pattern that would allow multiple solutions, which violates the uniqueness rule in Sudoku because if B1 is 3, B3 and E1 must be 8, making E3 a 3. But if B1 is 8, then, the answers change, and the puzzle can't have more than one solution.

This results in what some refer to as a "deadly rectangle" because it kills your puzzle. These deadly patterns can't exist, so if you find one, you can use logic to eliminate candidates and break up the pattern.

A Common Unique Rectangle Mistake

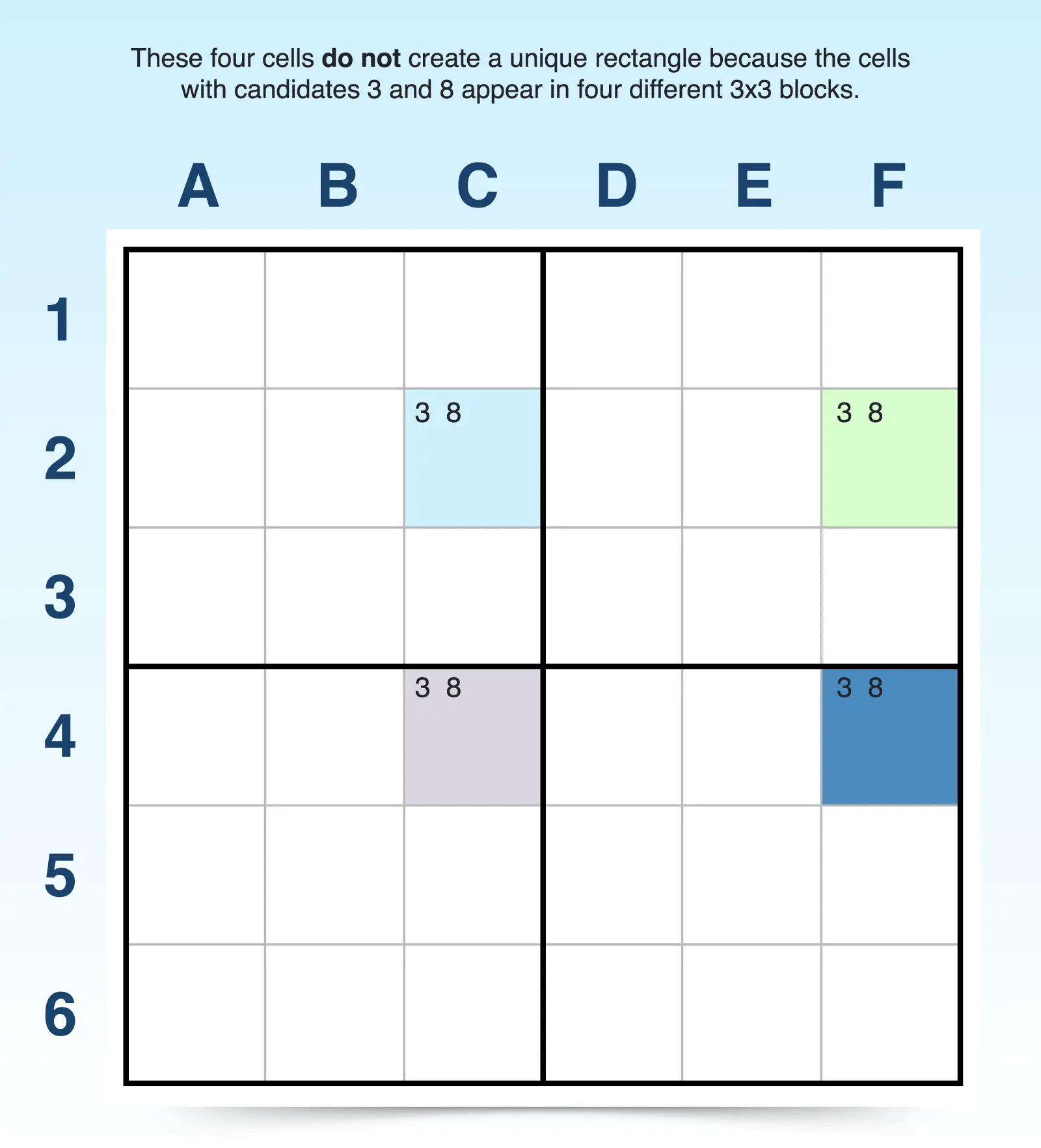
A common mistake in finding a unique rectangle is forgetting that cells must not violate the two blocks rule from the third step. If, for example, the cells create a rectangle but appear in four different blocks, those four cells don't propose two different solutions.

For example, C2, C4, F2, and F4 look like they could be a unique rectangle, but because they reside in four different 3x3 blocks, they violate the rule in Step 3. However, if you do find this pattern in four different blocks, you haven't wasted your time. You very well may have found another useful pattern, the X-wing.

Examples of Unique Rectangle Types

If you find a pattern in a Sudoku puzzle that results in more than one solution, you must find ways to break the pattern, also referred to as a "deadly pattern," and that's where identifying the different types of unique rectangles can help.

The different types offer different ways to break the deadly pattern and discover answers for cells or eliminate candidates. This solving technique can often take a shortcut through other logical, but more complicated, elimination techniques, helping you solve puzzles more efficiently and avoid potential deadly patterns.

Note that if you find a unique rectangle made up of naked pairs, you've gone wrong somewhere in the puzzle because you're stuck with four cells that can make up two different solutions.

Type 1

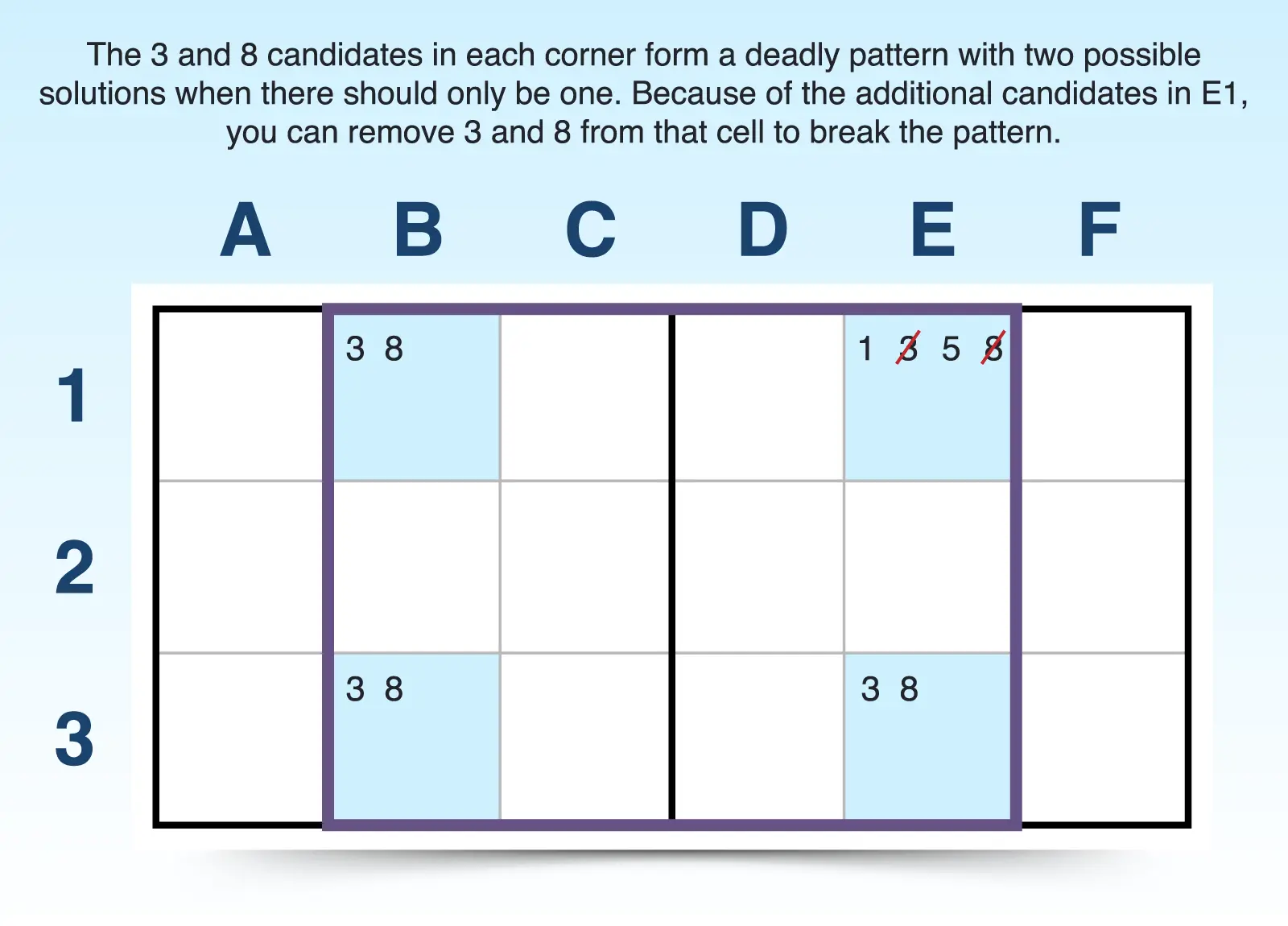
A Type 1 unique rectangle is the most basic, and all other types build from this foundation. You're likely to spot this more often in beginner puzzles. In this type, three cells have the same two candidates only, and the fourth cell has one or more additional candidates. For example, B1, B3, E1, and E3 all have the same two candidates in two rows, two columns, and two blocks, but E1, the fourth corner of the rectangle, has additional candidates (1, 5).

the

You can break up the pattern and create a unique solution because of the additional candidates. Since 3 and 8 can't be the answer in E1 without setting the stage for two solutions, you can safely eliminate the common candidates (3, 8) from E1.

Type 2

A Type 2 unique rectangle is similar to Type 1, but it has two cells with the same extra candidate with those two cells residing in the same row or column. In other words, the two cells are not diagonal from each other.

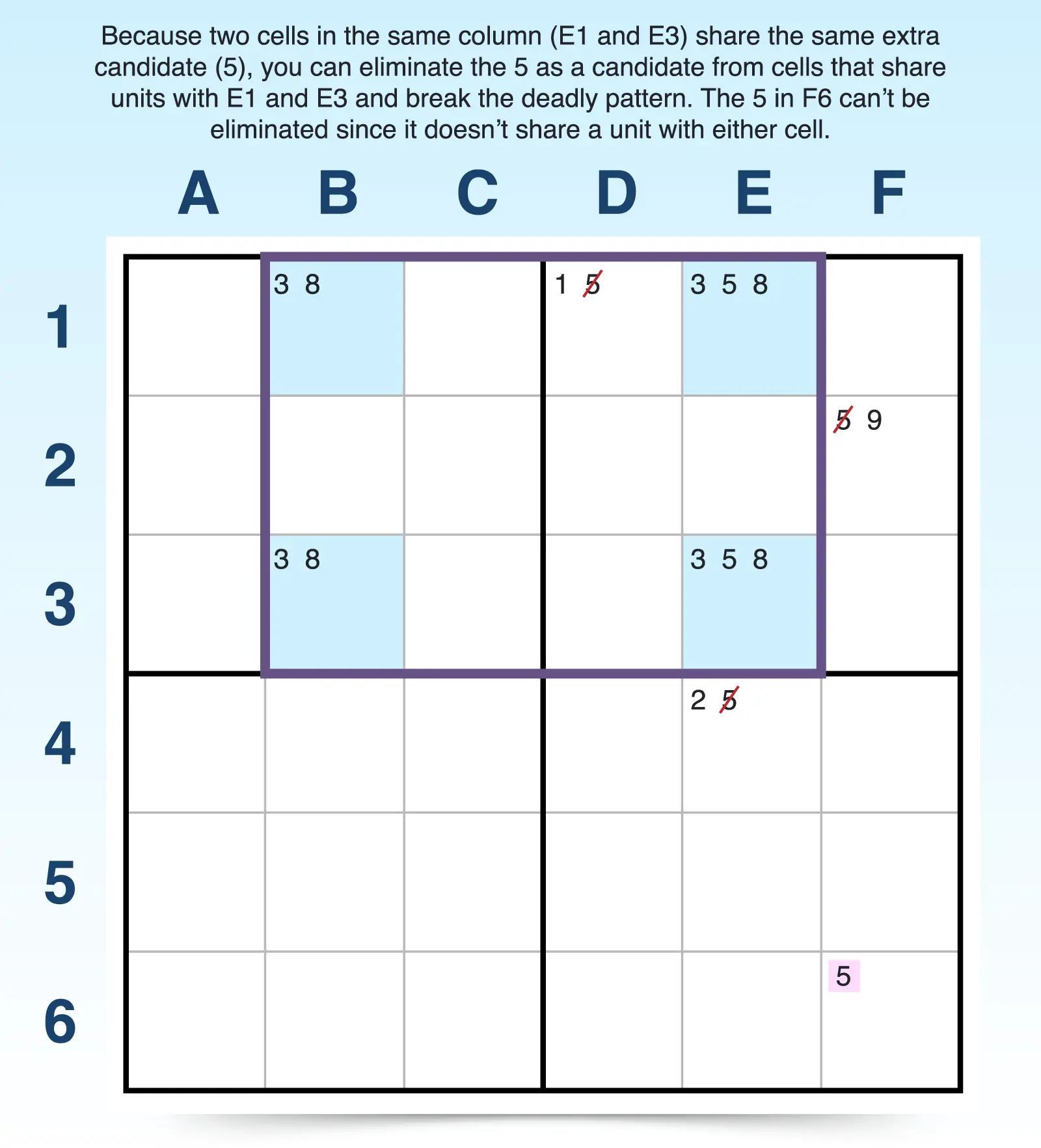
For example, B1, B3, E1, and E3 have the same two candidates (3, 8) in all four cells. But E1 and E3 have the same extra candidate (5), and those two cells are in the same column.

Some will refer to the two bi-value cells (one with just two candidates) as floor squares and the two cells with extra candidates as roof squares.

Because the two cells with an extra candidate in this type are in the same row or column, the pattern can be broken - the extra candidate forms a strong link because it must be the answer in one of the cells in that unit, so it acts like a conjugate pair. That means you can eliminate the extra candidate from other cells that both of the two cells see (cells that share a unit with them) because it cannot be a candidate in those cells.

For example, E1 and E3 have the same extra candidate and reside in the same column. So the 5 must be the answer in one of these cells to create a unique solution. Thus a 5 cannot be an answer in any other cell that E1 and E3 share a unit with.

So the 5s can be eliminated from D1 and F2 because they share the same 3x3 block with E1 and E3, and E4 can have its 5 eliminated since it shares the same column with E1 and E3. However, the 5 in F6 cannot be eliminated because it doesn't share a unit with those two cells.

When the two cells that share the extra candidate are in the same 3x3 block, you can eliminate many more candidates then when they simply share a row or column only.

Type 3

Type 3 unique rectangles add another layer to the Type 2. Like the Type 2, two of the four cells contain extra candidates and share the same unit. But in Type 3, there must be two different extra candidates, and they can appear in either or both of the cells. For example, one cell might have both extra candidates, or each cell might have one of them.

In the puzzle below, B1 contains the first extra candidate (4), and B3 has a second extra candidate (9). So in this unique rectangle, two extra candidates appear in two cells in the same unit (column B).

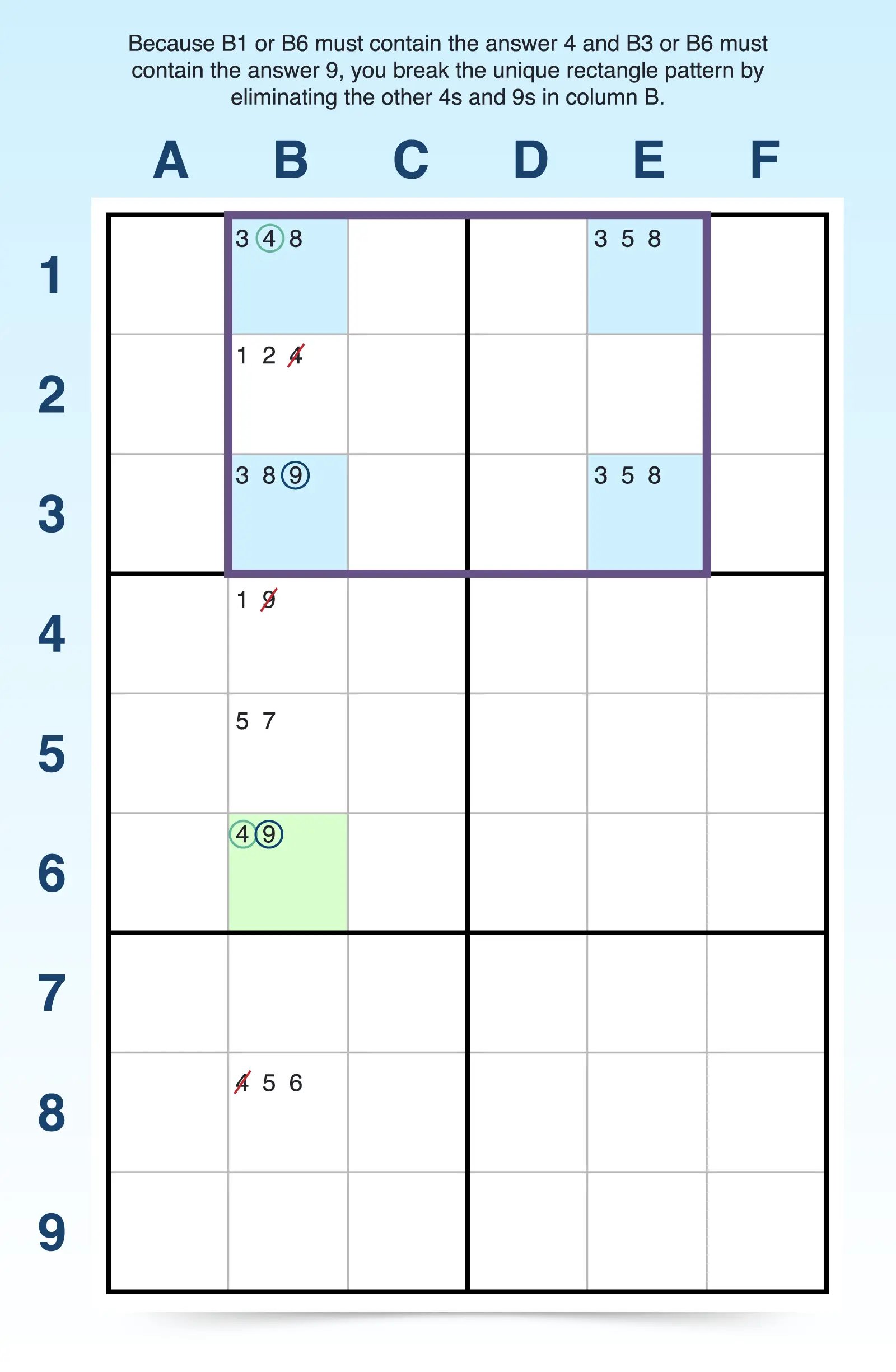
These extra candidates can help break the deadly pattern, but only under the right conditions. To trigger eliminations, you must also find a bi-value cell elsewhere in the same unit that contains both extra candidates. For example, B6 is a bi-value cell that contains both of the extra candidates (4, 9).

When that bi-value cell exists, you can treat the extra candidates in the rectangle and the bi-value cell as a locked set. This allows you to eliminate the same two candidates from any cells contained in that unit and break the deadly pattern.

For example, 4 must be an answer in either B1 or B6, and 9 must be an answer either B3 or B6. That means, in column B, 4s and 9s can be eliminated in other cells within that unit.

Type 4

Type 4 unique rectangles give you an opportunity to eliminate one of the common candidates in the cells that make up the unique rectangle. In this formation, two of the cells in the unique rectangle pattern that share the same unit (row or column) must be a naked pair, and the other two must have extra candidates, which can be the same or different numerals.

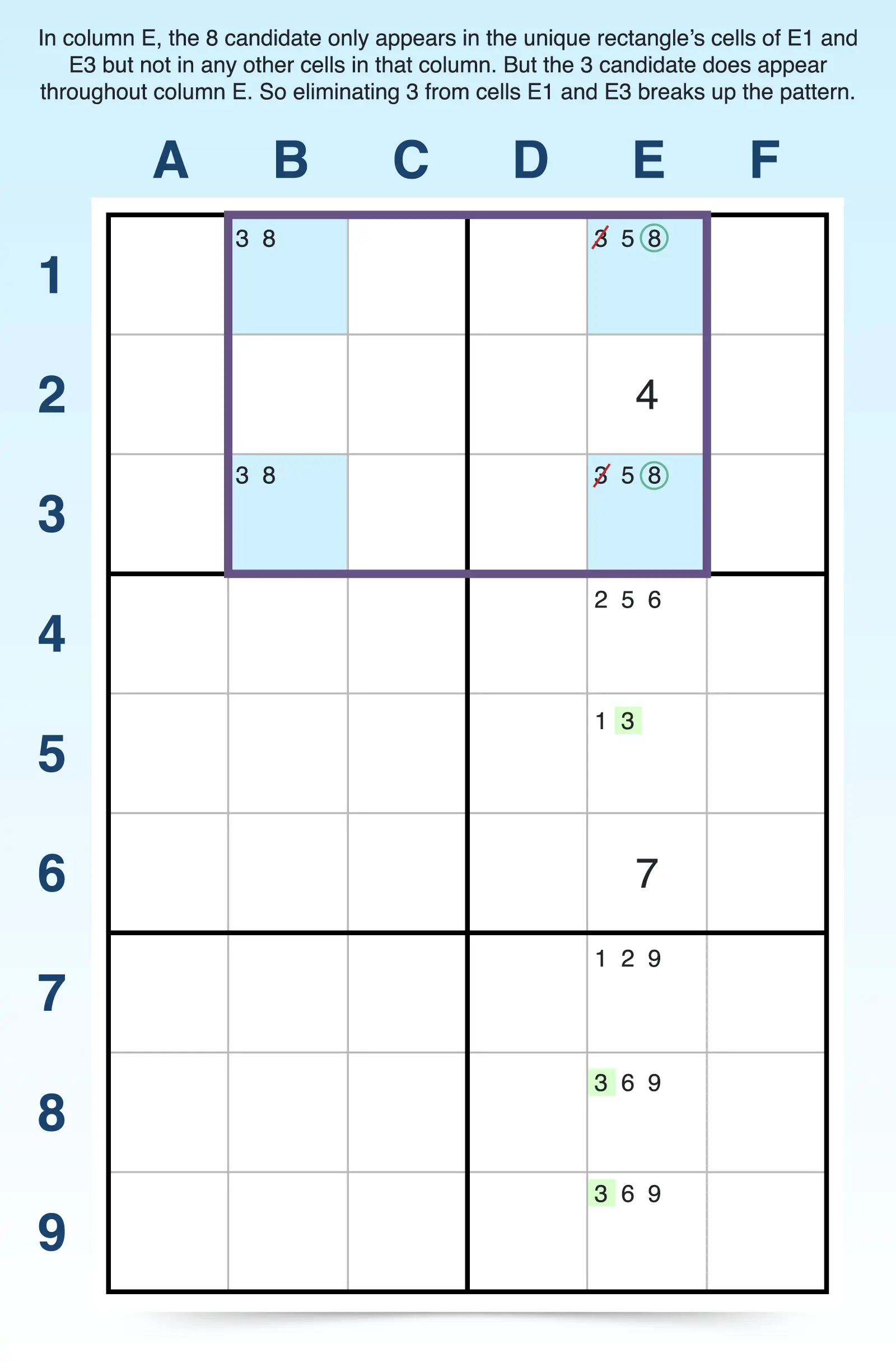
To find an elimination, focus on the unit (row or column) shared by the two cells with extra candidates. If one of the shared candidates appears elsewhere in that unit, but the other does not, then the one that does not appear must be the correct solution for one of the two cells in the unique rectangle. This allows you to eliminate the other candidate from both cells.

For example, in column 3, 3 appears outside of the rectangle cells, but 8 does not. So 8 must be the solution in either E1 or E3, which means 3 can be eliminated from both E1 and E3.

Type 5

Type 5 unique rectangles are similar to Type 2, but instead of the two cells that share the extra candidate falling in the same row or column, they are diagonal from each other (reside in opposite corners of the rectangle). For example, B3 and E1 both contain the same extra candidate (5).

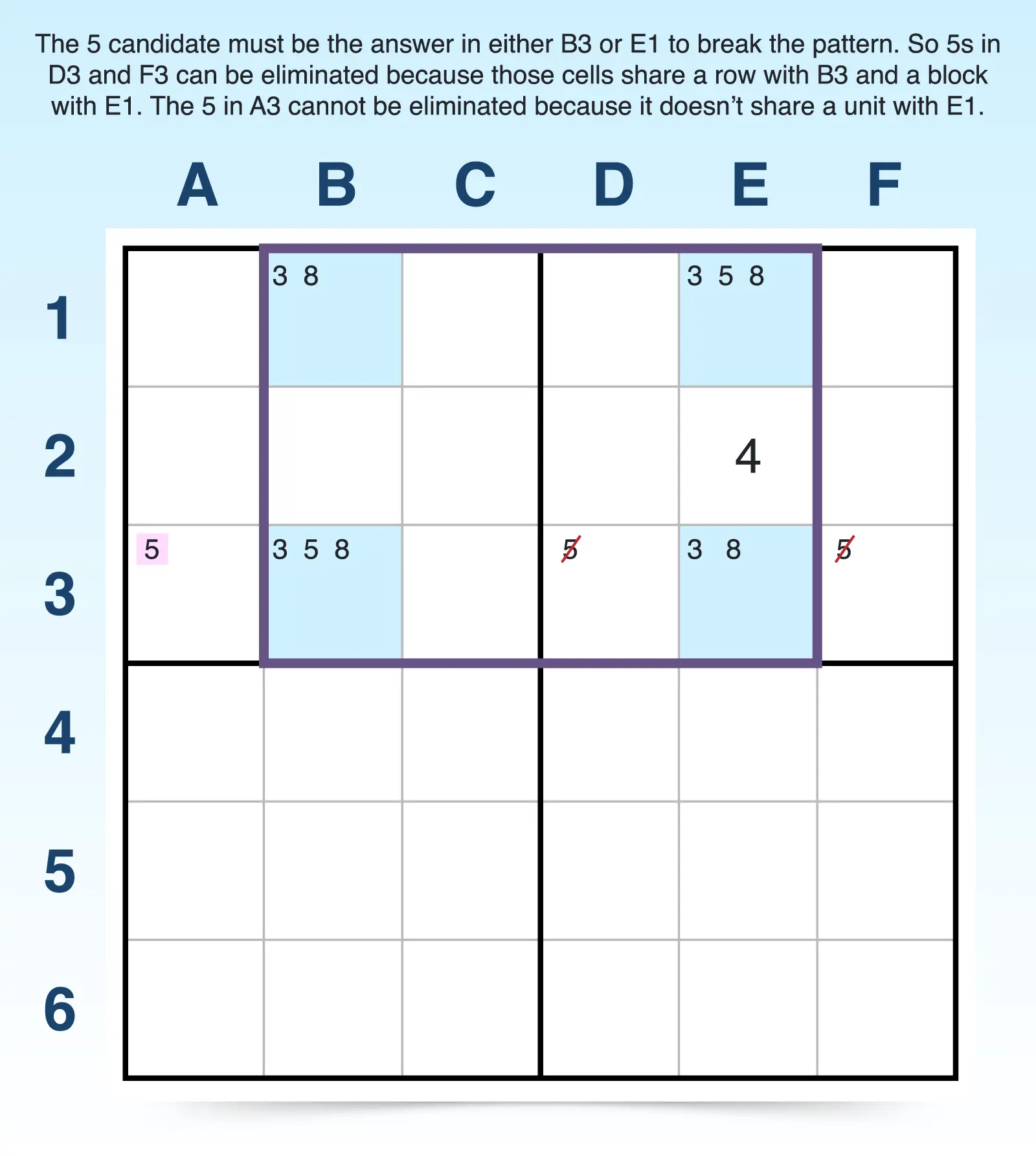
Similar to Type 2, you can eliminate the extra candidate from any cells that can see both of those diagonal cells. For example, D3 and F3 both see B3 (same row) and E1 (same block), so 5 can be eliminated from those cells. However, the 5 candidate in A3 only shares a unit (row 3) with B3 and doesn't share a unit with E1, so it can't be eliminated.

After you've mastered the most basic Sudoku strategies, unique rectangles offer enough variants to come in handy for numerous levels of puzzling. Whether you're a beginner upskilling to medium puzzles or you're an advanced solver working on more complex expert puzzles, identifying and using different types of unique rectangles can help you solve more puzzles more efficiently!