Finding these slick Y wing styles,
May seem so full of trials.
These tools, kindly please peruse,
As puzzles they oft abuse.
If you are not familiar with what is meant by Y wing styles, you may wish to visit
that blog page. Also, if you are not familiar with my standard puzzle mark-up, you may wish
to visit Forbidding Chains 102 The Practice. Finally, if I use a term that is not
familiar to you on this page, that term is proably defined in the Definitions page.
Links to both of these can be found to the right, under Sudoku Techniques.
Y wing styles are very much like a Y wing, just more general.
- A Y wing considers exactly three native strong sets, all of which are strong in
cells. Each cell is strictly limited to two candidates each. It can be viewed
as a Y, with two endpoints and a vertex.
- A Y wing style considers exactly three native strong sets. It does not limit
what kind of strength one uses. It can also be viewed as a Y.
Enhanced Puzzle Mark-up
In order to reliably find Y wing styles, the puzzle mark up indicated previously needs some
minor enhancement.
- Add an underline, or whatever suits you, to a candidate strength in a house if
that candidate at that cell either exists there or at the intersection of two houses.
- If the existence of that candidate in the house will see a cell that but for
that candidate would be solved, also add a V that points towards that cell
General types of Y wing styles
I hate to name techniques, as they are all really just forbidding chains. Nevertheless, it
is valuable to realize that Y wing styles fall into eight specific categories. In each of these
categories, exactly three strong sets are considered.
- 3 strong cells, 3 total candidates
- 2 strong cells, 1 strength in location (house), 2 total candidates
- 2 strong cells, 1 strength in location, 3 total candidates
- 1 strong cell, 2 strengths in location, 2 total candidates
- 1 strong cell, 2 strengths in location, 3 total candidates
- 3 strengths in location, 1 candidate
- 3 strengths in location, 2 candidates
- 3 strengths in location, 3 candidates
Three strong cells
This pattern can be further sub-divided by the number of houses that contain it.
- All cells are in one house - this is just a naked triple
- Vertex shares a house with each of the endpoints, two total houses. Each cell
has exactly two candidates - this is just a standard Y wing
- Vertex shares a house with each of the endpoints, two total houses. The endpoints
have two candidates each. The vertex contains 3 candidates. The two houses intersect
at three cells within the vertex house. This is a standard Almost Locked Set
configuration
There is little strategy to finding these three, as they have the most obvious type of strength.
Merely look from a potential vertex for two properly configured endpoints. It maybe easier
to start with a cell labelled AB, look for a cell AX,BX, or ABX, in the same house. Suppose that
you find AX. Now look for XB in the same house as AX. If you find ABX, look for AX or Bx, in the
same house as ABX, and with a viable intersection within that common house.
2 strong cells, 2 total candidates, one strength by location.
The only type of Y wing style that is easier to find than this one is a naked triple. It is
by far easier to spot than a Y wing. It is also much more common than a remote pair. Parameters:
- Find two cells containing only the same two candidates each. These cells must
not share a house, or they would be already a naked pair.
- Find a strong bridge between the two candidates. This bridge will involve one
of the two candidates. This bridge is the vertex of the Y wing style.
Example of 2 strong cells, 2 total candidates, and a bridge
g1=24 and h9=24 are the endpoints
g5=2 OR h56=2 is the vertex, or bridge
h1=4 and g9=4 are eliminated
The puzzle mark-up would underline g5=2, and place a V on it pointing at h9
The native strong sets considered are
- cell g1 = 24
- cell h9 = 24
- {g5=2, h56=2} in box h5
Example of 2 strong cells, 3 candidates, 1 strength in a house
Key:
- Black containers = endpoints of strong sets
- Black lines = strong links
- Red lines = weak links
- * = wild card
- green -1 is the available elimination
Here, c3 = 79 is the vertex. The elongated black box at c456 serves to indicate that
9 could be in any or all of those three cells. But, 9 cannot be at b456, a45. A puzzle
mark-up would underline a6=9 with a
V pointing at c3.
Native strong sets:
- cell a1=17
- cell c3=79
- {a6=9,c*=9} in box b5
1 strong cell, 2 strengths in location, 2 total candidates - as a nice loop
With this example, all three strong sets are both vertex and endpoint. This could be
called a Hub and Spoke. In that case, c1=hub, as it has two strong spokes:
- c1=9 == a1=9
- c1=1 == a12=1
coming from it. The puzzle mark-up would:
- circle the 9's at a1,c1.
- underline and V the 1 at c1
Typically, in this situation, a mirror will exist for the strong cell in a different house.
Here, a8=19, and it is mirrored by the hub c1 with strong 19's coming from c1.
The candidates with the green lines above them in this illustration are eliminated.
Above, the native strong sets considered are:
- cell a8=19
- {a1=9, c1=9} in box b2
- {c1=1, a12=1} in box b2
1 strong cell, 2 strengths in location, 3 total candidates
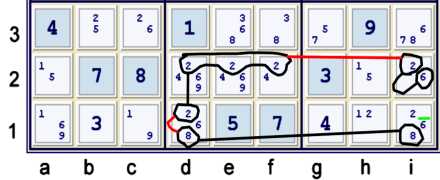
The example above is fairly typical of this Y wing style. The 2's in box e2 form the vertex.
The 8's in row 1 and the cell i2=26 form the endpoints. The 6 at i1 is eliminated.
The puzzle mark-up would circle the 8's in row 1 and underline and V the 2 at d1.
The native strong sets considered above are:
- cell i2=26
- {i1=8, d1=8} in row 1
- {d1=2, def2=2} in box e2
3 strengths in location, 1 candidate
This type of Y wing style is merely a forbidding chain on one type of candidate. As such,
it is more properly detailed in the page on coloring. Finding this type of Y wing style requires
only to concentrate on one type of candidate at a time, and should probably be done before
searching for other Y wing styles.
3 strengths in location, 2 candidates
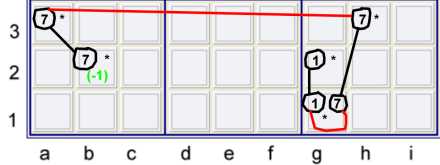
In the example above, only the 1 at b2 is eliminated. The chain would eliminate a 7 from
g2, but none can exist there since g1=7 == h3=7. Those 7's form the vertex. The puzzle mark-up would
circle all the 1's and sevens used above.
The native strong sets considered above are:
- {g2=1, g1=1} in box h2 (also would be in column g)
- {g1=7, h3=7} in box h2
- {a3=7, b2=7} in box b2
Suppose for a moment, though, that the 7's in box h2 were limited to g1 and ghi3 rather than
g1 and h3. This would still allow the elimination, but make finding the Y wing style much harder.
Suppose further that the 7's in box b2 were limited to b2, abc3. Again, still a valid elimination,
but harder yet to find. Suppose finally that the 1's in box h2 were limited to g1,ghi2. Now, the
elimination is still valid - but practically impossible to locate using any puzzle mark-up.
In this worse case scenario, the only real clue to look for this chain will be the very faint
strong spokes that come from g1. I suspect that I quite often miss this Y wing style when it is configured
in the worst possible way.
3 strength in location, 3 candidates
This Y wing style is usually not hard to find. The 9's are the vertex, and will always be
circled in the puzzle mark-up. Furthermore, the 1's would always be circled, so one cell, in
this case c1, will have two circles in it. The 6's could be a compound argument, and may have
only an underline at one end of the vertex. The native strong sets considered are:
- {c5=1,c1=1} in column c
- {c1=9,a1=9} in box b2
- {a1=6, c3=6} in box b2
There is one more sub-type of Y wing style that involves 3 strengths by location. It is
called a Hidden Triple.
Summary
Usually, Y wing styles are as easy, or easier, to locate than Y wings. Moreover, they are
much more likely to exist. The tendency across the web to devalue strength in location is a
clear error, if one wants to logically solve the truly tough puzzles. As I noted in the
comments after a previous blog page, 75% of the puzzle information is strength in location.
Any well thought out attack on a truly tough puzzle should not ignore such a large portion of
the available information.
The extension of these same ideas to forbidding chains with more than 3 strong sets is done
easily, but with each added layer of strong sets, the potential combinations expand rapidly. I
suppose one could be trite and say they expand exponentially, but the true accounting of how
rapidly they expand is better reflected in an obscure generating function.
I may expand this page later to include puzzles that solve easily with Y wing styles. Some
already are listed on the first Y wing styles page. One such puzzle not listed there is
Tough puzzle of February 9, 2007.
A longer list, as suggested:
The blog deals specifically with the puzzles listed above.