The following is an illustrated proof for the
Tough Sudoku of March 07, 2007.
There are many ways to tackle this one. The primary focus of this page is to illustrate
using Forbidding Chains, also called Alternating Inference Chains or AIC.
This puzzle can extensively use a special type of such chains, that I call wrap around.
These are also called continuous nice loops. In such a chain, the endpoints of the
chain are in conflict with other, often allowing one to make multiple disparate eliminations.
You may need to refer to previous blog pages to understand
this proof. Links to these pages are found to the right, under Sudoku Techniques.
At many times during this illustration, there are other steps available. It is not the goal
of this page to show every possible step, but rather to illustrate steps that, taken together,
unlock this puzzle
The information on the following blog pages is required to understand this page:
The illustrations of forbidding chains used on this blog page will share the same key:
- black lines = strong links
- red lines = weak links
- candidates crossed out in red = candidates proven false
- candidate groups will be circled together using black containers
Many steps that are possible will not be shown to keep the page as short as possible.
However, every step that is shown can be justified by considering only the previous illustrated
steps.
Puzzle at start
A few Unique Possibilities are available here.
- f5 = 8% cell
- d9 = 6% box & row
- b5 = 6% row
- c1 = 5% box
- b2 = 1% column
The puzzle is advanced to 27 cells solved. (UP 27)
Pair 37
Illustrated to the left is the Forbidding Chain representation of Naked Pair 37 at de5.
As a Forbidding Chain:
- d5=3 == d5=7 -- e5=7 == e5=3
- => gh5≠3 & cg5,d6≠7
In the chain above, since e5=3 and d5=3 conflict with each other, all the weak links are proven
strong, justifying all the eliminations.
Hidden Pair 37
Illustrated to the left is the Forbidding Chain representation of Hidden Pair 37 at d35.
As a Forbidding Chain:
- d3=3 == d5=3 -- d5=7 == d3=7
- => d3≠15
In the chain above, since d3=3 and d3=7 conflict with each other, all the weak links are proven
strong, justifying all the eliminations.
One can of course justify the last eliminations by alternatively finding the naked triple
159 at d689. Also, as noted many times in this blog, even though it is true that d5=3 == d5=7,
it is also true that d5=3 -- d5=7. There is never any requirement that weak and strong be
mutually exclusive properties.
Why bother with a forbidding chain representation of such simple ideas? Quite simply, all
techniques are a subset of Forbidding Chains. Furthermore, understanding that techniques one
uses all the time are actually Continuous Nice Loops, or Wrap Around Chains, is helpful in understanding
other such Nice Loops.
Current Puzzle
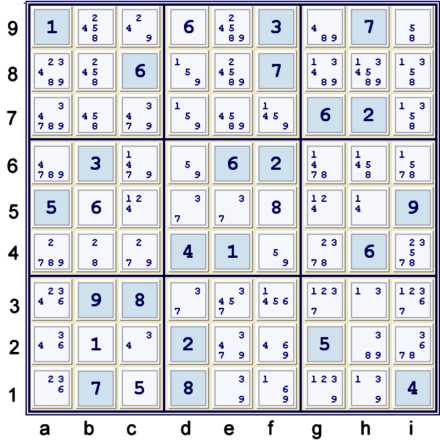
The current puzzle state has revealed an Almost Unique Rectangle 37 at de35. One can
immediately eliminate 37 from e3. This by itself leads to no cell solutions. Furthermore,
once one uses this step, one can no longer prove that the solution one finds is the only
solution. I try to avoid using AURs whenever possible. Nevertheless, one may think of
the AUR 37 as a clue - e3=37 can likely be eliminated.
There are a few more steps one can take at this point (Some Locked Candidates and a short
depth 2 coloring elimination with 5s). Since none of these steps further the puzzle significantly,
to save time and space, they are not taken in this proof.
Puzzle Marks
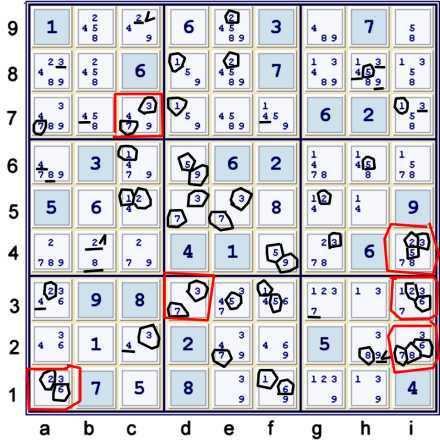
Illustrated above is my normal puzzle mark-up. All bivalue by location candidates are circled
black. The underlined candidates are a special type of bivalue strength relative to a house. The
black V's point towards cells that will be solved if an underlined candidate does not exist. The
red circles are cells of interest due to remote pair-like potential, or because of 3 black circles
in one cell.
There seems to be much potential action in the bottom third of the grid. I can assure you,
that almost every indicated location to search will yield some sort of fruitful chain. This
puzzle, unlike the Monsterously Diabolical Tough Puzzle of February 20, 2007, is easily solved
using any of a great number of available Forbidding Chains.
Most of the Chains that I found end up proving that i3=6. One can easily see that if i3=6,
the puzzle will have a whole cascade of Unique Possibilities, as then:
- i4 = 2% column => i4≠35 => some cells will equal 3,5.
- Also, b4≠2 => b4=8.
to name a few. The primary idea of the puzzle mark-up is twofold:
- Identify likely locations for Chains
- Identify likely Fruitful Chains - ones that will solve some cells
A Wrap Around or Continuous Nice Loop Chain considering 5 strong sets
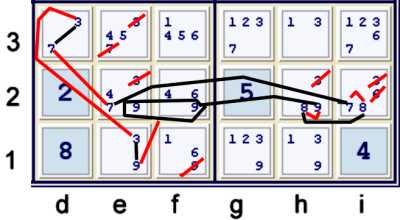
Consdering only 2/9s of the puzzle grid, one can find a very powerful wrap around forbidding
chain. Illustrated above, the only thing a bit complex about this chain is the grouped
consideration of candidate 9 at h2 versus ef2. Note that the puzzle marks underlined h2=9
with a V pointing towards cell e1=39.
One can start this chain at any strong set considered above. Here is one way:
d3=3 == d3=7 -- e2=7 == i2=7 -- i2=8 == h2=8 -- h2=9 == ef2=9 -- e1=9 == e1=3
Since d3=3 and e1=3 are in conflict with each other, this chain is a wrap around chain.
Every weak link above is thus proven strong, giving us 5 new strong sets:
- d3=7 == e2=7 => e3≠7
- i2=7 == i2=8 => i2≠36
- h2=8 == h2=9 => h2≠3
- ef2=9 == e1=9 => f1≠9
- Chain endpoints: e1=3 == d3=3 => e23≠3
Since i2≠6, i3 = 6% column and box, yielding a cascade of Unique Possibilities to 59 cells
filled.
Try a proof by contradiction with any of the forbidden candidates. It will show a contradiction
within at least one of the 5 strong sets considered
- d3=37
- e1=39
- ef2,h2=9
- hi2=8
- ei2=7
The value, though, of understanding the forbidding chain is:
- One gets all the eliminations listed at once!
Otherwise, one might require seven different proofs by contradiction to get the same result!
An alternate depth 5 continuous nice loop
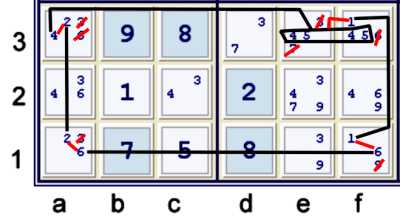
The chain illustrated above is perhaps harder to see. It is very common that if there exists
one continuous nice loop forbidding chain, there are other ones availabe using completely different sets,
but forbidding some of the same items. This chain could be written as:
{Hidden pair 415 at ef3} ==1 a3=4 -- a3=2 == a1=2 -- a1=6 == f1=6
-- f1=1 == f3=1
Since f3=1 and ef3=Hidden Pair 45 are in conflict with each other, this is again a nice loop
chain whereas all the weak links are proven strong:
- {Hidden pair 45 at ef3} == f3=1 => f3≠6 and e3≠37
- Again, the potential AUR eliminations are made by the chain, without using Uniqueness!
- a3=2 == a3=4 => a3≠36
- a1=2 == a1=6 => a1≠3
- f1=6 == f1=1 => f1≠9
Note that some of the same eliminations are made by each of the two chains I choose to illustrate.
After making the indicated eliminations, i3 = 6% row, and the cascade of Unique Possibilities occurs
again leading to exactly the same puzzle with 59 cells solved.
The 5 strong sets considered by the graphic above are
- a3,ef3 = 4
- ef3 = 5
- a13 = 2
- af1 = 6
- f13 = 1
Although one may find the last chain illustrated above more difficult to see, I judge them
to be about equivalent. The power of using Almost Locked Hidden Sets is quite interesting,
and worth the trouble trying to understand.
I suppose it is interesting that both chains solve i3, and that both eliminate e3=37, and
that both eliminate f1=9, and that both chains make exactly seven eliminations.
Again, one can do a proof by contradiction, but one can easily miss some of the eliminations
by doing so. I highly recommend understanding forbidding chains for precisely this reason.
One of the main reasons that I have chosen using forbidding chains as my vehicle for proving
and solving Sudoku Puzzles is precisely these types of chains, which can yield
multiple eliminations that seem unrelated.
Puzzle at UP 59
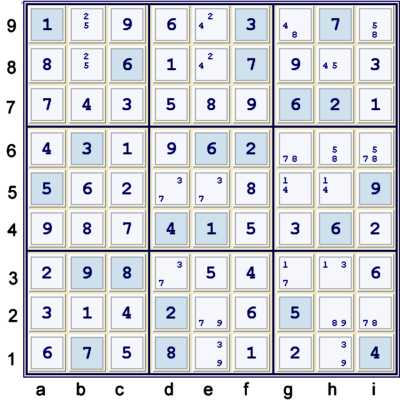
After only Unique Possibilities, the puzzle is advanced to the state shown above. Here
we have an interesting configuration, whereas all but one cell, i6, is limited to exactly
two possible values. This is called a BUG - meaning BiValue Universal Grave.
In a BUG, one uses Uniqueness of Solution to attack the cell with 3 possible values left.
It is very rare that using BUG is required to unlock a puzzle. In the case above, BUG implies
that cell i6=8, and one can easily decide that by seeing that only 8's are not bilocation
in column i, row 6, and box h5.
Instead of using BUG, there are dozens of other manners to attack this puzzle at this stage.
There is at least one Y Wing, and many Y Wing Styles. Very
common Y wing styles are indicated by the almost remote pair like 58 at i9h6 or 78 at i2g6.
Both of these will eliminate one of the values from the cell i6 and solve the puzzle. I will
only demonstrate one, as one is all one needs.
Very Common Y Wing Style
Consider g69 = 8 as the vertex.
h6 = i9 = 58 as endpoints
Eliminates h8,i6=5.
As a chain:
- i9=5 == i9=8 -- g9=8 == g6=8 -- h6=8 == h6=5
- => i6,h8≠5
The puzzle now easily solves.
Find Naked Singles to the end.
Solved Puzzle
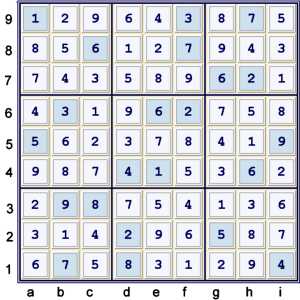
Proof
- Start at 22 filled - the given puzzle. Unique Possibilities to 27 filled. (UP 27).
- Naked pair 37 at de5 forbids gh5=3, cg5d6=7
- Hidden pair 37 at d35 forbids d3=15
- i2=8 == h2=8 -- h2=9 == ef2=9 -- e1=9 == e1=3 -- d3=3 == d3=7 -- e2=7 == i2=7
- forbids i2=36, h2=3, f1=9, e23=3, e3=7. UP 59
- very common Y style i9=5 == i9=8 -- g9=8 == g6=8 -- h6=8 == h6=5 forbids i6,h8=5 UP 81
- Sets: 2 +2 + 5 + 3 = 12
- Max depth 5 at 2.3
- Rating: 2(.03) + .31 + .07 = .44
Hopefully, this proof demonstrates well not only the power of forbidding chains, but also
the power of understanding them well!