The following is page three of an illustrated proof for the
Tough Sudoku of February 20, 2007.
This is page three of a multi-page proof for this puzzle. The pages will come out gradually over
the next few hours, as they are created. The general theme of each page will be slightly different,
as the puzzle progresses through various degrees of technique difficulty.
You may need to refer to previous blog pages to understand
this proof. Links to these pages are found to the right, under Sudoku Techniques.
The information on the following blog pages is required to understand this page:
The illustrations of forbidding chains used in this proof will share the same key:
- black lines = strong links
- red lines = weak links
- black circles connected with black lines = multi-part strong sets
- candidates crossed out in red = candidates proven false
Conventions used in writing Forbidding Chains
The following convention will be used when presenting complex or
Advanced Forbidding Chains:
- A == B -- C ==1 {D == E -- F ==1 G} -- H == I
- subscripts will be used to label a stong link that is conditional, meaning in
the case above, for example, that {C,F,G} form a native strong set
- {}'s will contain a sub chain. Generally, subchains are conditional. In other words,
the entire sub-chain either exists, or it does not exist, dependent upon the subscripted
internal links. In the case shown above, both D and G must forbid H in order for the
sub-chain within the brackets to be a valid piece of the chain. Whether or not the
sub-chain is eventually proven false or true makes no difference to the validity of the
larger chain, as with any other Boolean used in the chain.
- As in all properly written forbidding chains, one can read the chain either
left to right or right to left
Suppose in the example above that one substitues {D == E -- F ==
1 G} with the Boolean
Z. Then one would have:
- A == B -- C == Z -- H == I
In all cases, Z must be true if C is false.
In most cases, both endpoints of Z must forbid H. However,
in the special case whereas Z is a wrap-around or nice loop chain, as long as at least one
of the newly proven strong sets within Z forbids H, all is good. This is no different than
using Almost Locked Sets within a Chain, except that there is no requirement that a subchain
be only a conditionally Locked Set.
Realizing the validity of using any Forbidding Chain as a Boolean within a Forbidding Chain
is the primary inspiration of all Net or 3-D techniques. One may
see them represented otherwise, but a strict adherence to the manner in which I employ such chains
keeps the chain integrity in both directions, and allows tremendous power in writing complex
techniques such as Sue de Cox with Forbidding Chains
Back to the puzzle
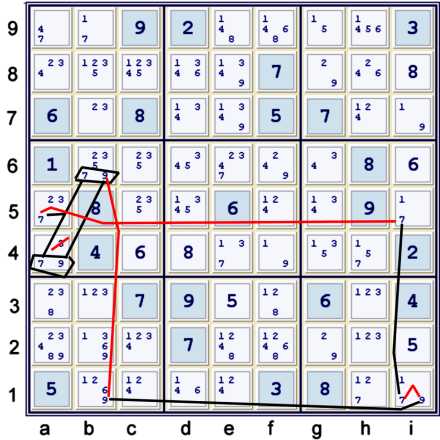
Above, a4 must be either 7 or 9. If a4≠79 then
- b6=9 and a5=7 =>
- b1≠9 and i5≠7 =>
- i1=9 and i1=7
This idea can be presented in a forbidding chain:
- {Hidden pair 719 at a4b6} ==1 a5=7 -- i5=7 == i1=7 --
i1=9 == b1=9 -- b6=9 == a4=9 => a4=79
In this case, the depth of the step is 4, as it considers exactly 4 native strong sets:
- a4,b6 = 9
- b1,i1 = 9
- i5,i1 = 7
- a4,a5,b6 = 7
It may appear upon first inspection that one is using 5 strong sets, but the chain actually uses
the first strong set that I listed twice. There is no reason not to do that!
Finally, one may think that the chain above is a wrap-around or nice loop chain. This is an error.
The endpoints of the chain are not in conflict with each other. a4=9 does not prevent b6=7, and
a4=9, b6=7 is one of two possibilities meant by Hidden Pair 79 at a4,b6.
The chain above has been available for quite some time. I choose to present it now, since the
chains that I will present on this page are meant to be very important to solving this puzzle.
A very tough chain to understand
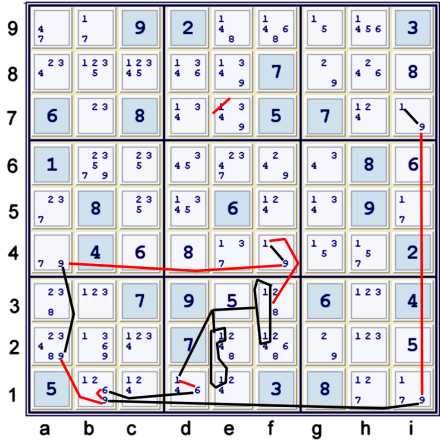
Hopefully, I can make the graphic above clear. The easiest way to understand, at first, is
probably with a contradiction proof:
- Suppose e7=1
- => e12≠1
- Now, if e12≠1 we have the following forbidding chain:
- b1=6 == d1=6 -- d1=1 == f23=1 -- f4=1 == f4=9 -- a4=9 == a2=9 forbids
b1=9
- but, b1≠9 => i1=9 ==> i7≠9 => i7=1. This contradicts e7=1
One can write this idea as a Forbidding Chain:
- e12=1 ==1 {b1=6 == d1=6 -- d1=1 ==1 f23=1 -- f4=1 == f4=9 --
a4=9 == a2=9} -- b1=9 == i1=9 -- i7=9 == i7=1 => e7≠1
The six strong sets considered are:
- i7 = 19
- bi1 = 9
- bd1 = 6
- f4 = 19
- a24 = 9
- d1,e12,f23 = 1
Of these strong sets, the ones that are indicated by the puzzle mark-up as points of interest
are all of them except the last one. To find such a chain, one has to think only one strong set
outside the box.
This elimination is a set up for the next elimination, which is not any easier.
Another very tough chain to understand
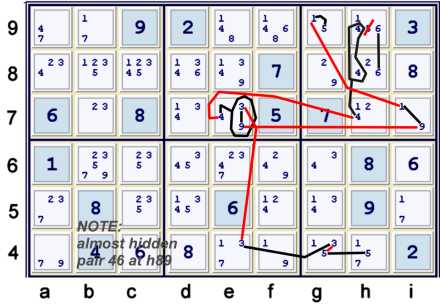
Again, it is probably easier to understand this chain through a contradiction analysis:
- Suppose h9=5
- => h9≠46 => h8=6 => h8≠4 => h7=4 => e7≠4 => the existence of this chain:
- g9=5 == g9=1 -- i7=1 == i7=9 -- e7=9 == e7=3 -- e4=3 == g4=3 forbids g4=5
- g4≠5 => h4=5 contradicts h9=5
The 5s and 1s are wrapped all up with each other here, so one can consider the exact same sets and
forbid g9=1, or g4=5, or add one set and forbid h4=17. As a forbidding chain, the graphic I choose
to illustrate can be written:
- {Hidden Pair 416 at h89} ==1 h7=4 -- e7=4 ==2
{g9=5 == g9=1 -- i7=1 == i7=9 -- e7=9 ==2 e7=3 -- e4=3 == g4=3 -- g4=5 ==
h4=5} => h9≠5
The seven strong sets considered are
- gh4 = 5
- eg4 = 3
- e7 = 349
- i7 = 19
- g9 = 15
- h789 = 4
- h89 = 6
Of these, only h789=4 and e7=349 are not indicated as likely suspects in the puzzle mark-up.
However, the entire box h8 has been indicated as a possible area of investigation for some time.
Finding such a chain may take some practice. One may have to learn the standard chains well.
Only after such study did the more complex chains become less obscure for me. I suppose there
are some relevant banalities that deal with human motor skills....
After making the indicated elimination, finally some cells can be solved:
- g9 = 5% box & row
- h4 = 5% box, row, & column
- i5 = 7% box
- h1 = 7% box, row, & column
Much work to get to UP 33!
Hidden Pair 79
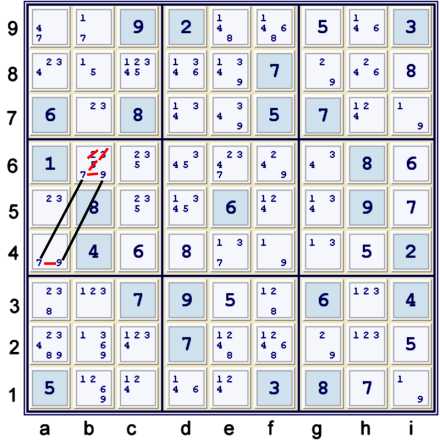
Graphically illustrated as a forbidding chain, one can find Hidden Pair 79 at a4b6.
One may find the naked triple 235 at a5, c56 easier to spot. In either event, b6≠235.
This solves one more cell:
Having arrived at UP 34, it probably is time to consider a new, or a completely refreshed, puzzle
mark-up. The struggle to solve this one continues on yet another page!
Please visit the next blog page on this puzzle to see some more steps!