These definitions are primarily provided so that if you visit other Sudoku sites, you can
understand the terminology commonly used there.
Examples
Almost Locked Sets - One degree of freedom


Almost Almost Locked Set - Two degrees of freedom
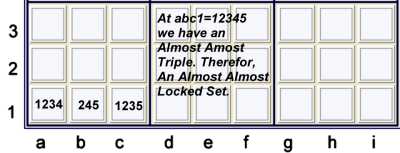
For the purposes of this page, one really only need consider Almost Locked Sets =
Tuples with 1 degree of freedom.
The general idea
Suppose that S is:
- A Naked Almost Locked Set (has one degree of freedom)
- Contains the candidate r
Then one could say:
- S is a Naked N tuple OR
- S contains candidate r
If this is not immediately obvious, consider:
- If S does not contain r, it is a naked n tuple
- S must either contain r, or not.
We could write this as part of a forbidding chain:
- (S is a naked ntuple) == (S contains r)
Simlarily, suppose that S is:
- A Hidden Almost Locked set (has one degree of freedom>
- contains the cell x
Then one could say:
- S is a Hidden N tuple OR
- S contains cell x
We could write this as part of a forbidding chain:
- (S is a hidden ntuple) == (S contains x)
Hopefully the symmetry is clear.
It should now be fairly obvious that one can use an Almost Locked Set configuration
within a forbidding chain.
Linking the idea
The idea of Almost Locked Sets is of little use unless it links with at least something else.
Clearly, since the idea of ALS is actually a strong link in the chain, it needs to link to
the rest of the chain using weak links. Really, this is all one needs to know. However, in the
common usage of this concept elsewhere, the protocol is to link one ALS to another ALS. This
restriction is hardly necessary. Below are some examples of linking two ALS's together.
Typical ALS examples
Y wing as ALS
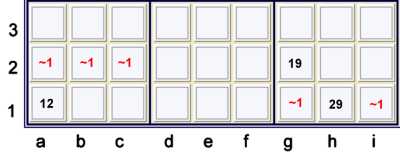
The example above is also commonly described as a Y wing. One can, however,
interpret this configuration as Two ALS's with a weak link between them.
- a1=12 is an almost single with one degree of freedom
- h1=29 and g2=19 is an almost pair with one degree of freedom
- a1=2 -- h1=2 links the two almost locked sets
- The 1's are therefor strong in one set or the other.
- Therefor, a1=1 == g2=1 forbids abc2=1,gi1=1
As a forbidding chain, rewritten to reflect the ALS:
a1=1 == a1=2 -- h1=2 == {Pair 9, 19 at h1,g2 respectively}
- proves a1=1 == g2=1, forbids abc2=1,gi1=1
This example is of little use if you understand a Y wing, but it is helpful in understanding
how techniques that seem unrelated are in fact closely related, if not identical.
Y wing style as ALS
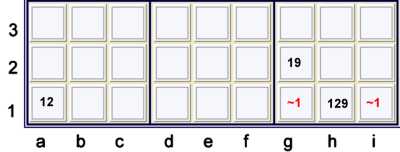
I have treated the example above previously as a Y wing style. Clearly,
a1=2 forbids h1=2. Therefor, a1=1 == {pair 19 at g2h1}.
As a forbidding chain, one could write:
- a1=1 == a1=2 -- h1=2 == {pair 19 at g2h1} forbids gi1==1
As an ALS logic, one would say:
- S1 = {a1=12}
- S2 = {h1=129, g2=19}
- Note that S1, S2 are both ALS with 1 degree of freedom
- Note that 2's are weak across sets S1, S2
- Therefor, {S1 contains 1} == {S2 contains 1}
- Therefor, a1=1 == {h1g2contains 1} forbids gi1=1
Almost Triple with Almost Pair
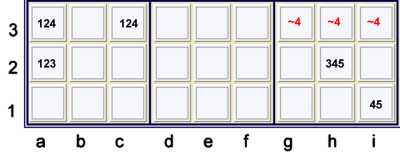
Key: Red ~4 means 4 is excluded by this pattern at these locations
Here we have:
Triple 12,124,124 at a2,ac3 respectively but for the possible 3 at a2
Pair 45 at h2i1 but for the possible 3 at h2
Since a2=3 and h2=3 cannot both occur, clearly:
- {Triple 12,124,124 at a2,ac3 respectively} == {pair 45 at g2i1}
- Forbids ghi3=4
As a forbidding chain:
- {Triple 12,124 at a2,ac3} == a2=3 -- h2=3 =={Pair 45 at h2i1} forbids ghi3=4
As ALS style logic:
- Let S1 = {a2=123,a3=124,c3=124} - note ALS with one degree of freedom
- Let S2 = {h2=345, i1=45} - note ALS with one degree of freedom
- 3 is a restricted common candidate across the sets S1,S2
- 4's are strong within the sets
- All cells seen by the 4's all the 4's within S1,S2 are forbidden
- Thus ghi3=3 is forbidden
The forbidding chain style of expressing this idea is more concise than the alternatives.
Almost Triple with Almost Hidden Pair
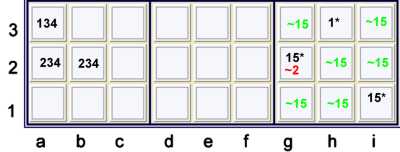
Key:
- Black marks = native strong cells with candidates listed
- * = wild card (could be any candidate(s)
- Green ~15 = cells that, as a native puzzle condition, cannot contain 15.
Therefor indicates strength in location for those candidates 15.
- Red ~2 = cell proven not to be 2
Here, we have:
- Hidden pair 15 at g2,i1 but for the possible 1 at h3
- Triple 34,234 at a3,ab2 respectively but for the possible 1 at a2
- Since a3=1 and h3=1 cannot both occur at the same time,
- {Hidden pair 15 at g2i1} == {Triple 34,234 at a3,ab2 respectively}
- forbids g2=2
As a forbidding chain:
- {Hidden pair 15 at g2i1} == h3=1 -- a3=1 == {Triple 34,234 at a3,ab2} forbids g2=2
If this one escapes you, then consider what if g2=2. Then pair 34 at ab2 would force a3=1, but
g2=5 == i1=5 would force i1=5, but the strong set{g2=1,i1=1,h3=1} would force h3=1. Clearly,
both a3=1 and h3=1 cannot occur. There is always an equivalent proof by contradiction available
for every possible sudoku technique.
Aligned Almost Triple with Almost Hidden Pair
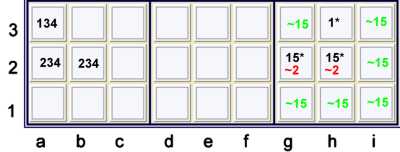
The example above is almost precisely like the previous one, but the location of
the Almost Hidden Pair 15 allows one to make an additional exclusion as illustrated.
Almost Hidden Pair with Almost Hidden Triple
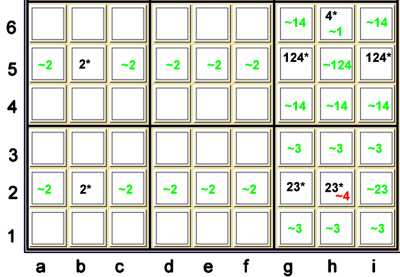
The example above is a bit complex. It is probably better understood with a bit more
chaining instead of using the Almost Hidden Triple, since we also have two Almost hidden Pairs.
As a forbidding chain:
- {Hidden pair 23 at gh2} == b2=2 -- b5=2 == {Hidden pair 12 at gi5} -- gi5=4 == h6=4
Logical extensions of the concept
If you consider the concept carefully, all strong sets on the puzzle grid are Almost Locked
Strong Sets with some degree of freedom. For this reason, the concept easily generalizes beyond
using only Almost n tuples, to also using, well, Almost Anything. Concepts that can be similarily
analyzed include (but are not limited to)
Almost Fish (Xwings, Swordfish, Finned Swordfish, Jellyfish, etc)
Almost Almost Unique Rectangles
Almost coloring
Almost Locked Candidates
Almost Forbidding Chains
Of these, the last one is the most interesting
An almost pair with an almost forbidding chain
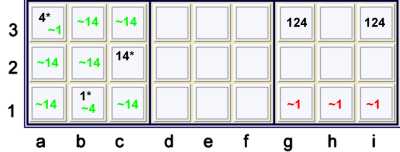
If you are very clever, you may see the pattern above as An Almost Pair strongly linked
to an Almost Hidden Pair. In this way, it is clearly also a subset of the general idea of
Almost Locked Sets. Nevertheless, that expression of this elimination is fairly clumsy. I
prefer to see it this way:
- b1=1 == c2=1 -- c2=4 == a3=4 -- gi3=4 == {Pair 12 at gi3} -- ghi1=1
An almost pair with an almost forbidding chain forming a wrap around forbidding chain
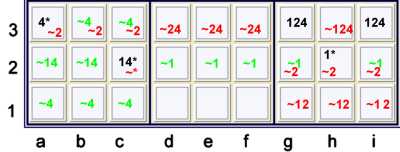
key
- Black marks are native strength in cells
- * is a wild card
- ~ means not
- Green marks indicate, by exclusion, native strength in location
- Red marks indicate items forbidden by the pattern
The exclusions above are justified by the following "wrap around", or closed loop, forbidding
chain
- h2=1 == c2=1 -- c2=4 == a3=4 -- gi3=4 == {pair 12 at gi3},
but {pair 12 at gi3} -- h2=1, therefor forbids
- c2=2356789
- ghi,h3=1
- defh3=4
- abcdefh3=2 and ghi12=2
There is much bang for the buck here. Because this is a wrap around chain, there are many
equivalent ways to present the same idea. An instructive, albeit not very transparent one is
:
- g3=2 == {Y wing style wrap around chain at hc2=1, c2a3=4, g3=14} -- i3=14 == i3=2,
but i3=2 -- g3=2, therefor forbids (same items listed in chain above)
This previous representation illustrates the almost infinite flexibility of using forbidding
chains, as it uses an Almost Locked Y Wing Style Chain and and Almost Almost Locked set.
Almost Hidden Pair with an Almost Forbidding Chain
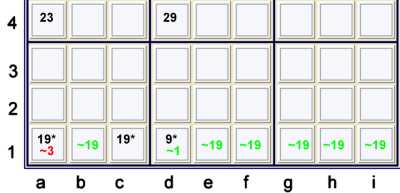
If you are clever, you may see the elimination above as an Almost Locked Hidden Pair used
with an Almost Naked Pair. That is a bit clumsy, so I prefer:
- {Hidden pair 19 at ac1} == d1=9 -- d4=9 == d4=2 -- a4=2 == a4=3 forbids a1=3
Summary
The concept of Almost Locked Sets is a very powerful one. The more generally one applies the
concept, the more powerful it is. In its most general form, it is equivalent to forbidding
chains, and probably can be used to justify every possible sudoku elimination. Nevertheless,
its representation can be a bit unwieldy, so forbidding chains are probably a better language
and logic system choice. However, since the concept allows one to easily take previously learned
techniques and apply them at will, it is a valuable concept to understand fully.
Some Practice Puzzles