Before diving into the Swordfish technique, make sure you fully understand the X Wing Technique as the Swordfish builds on that.
The idea behind X Wing extends easily:
- Consider any one candidate
- Consider any N distinct rows, N>0.
- Let the candidate be limited to no more than N cells in each of these N rows
- Let this group of no more than N^2 cells share exactly N columns
- The candidate is forbidden from all the cells in those N columns outside of those N^2 cells
Because of symmetry, one can exchange columns for rows in this
theorem.
With N=1, we have the trivial case of a Unique Possibility. With N=2, we have a standard
X wing. With N=3, we have a Swordfish. With N=4, we have a jellyfish.
with N=5, the creative name squirmbag is used.
To prove this technique, I prefer to use induction.
This technique merely crosses the possible locations of a candidate in N rows with N columns.
It is analogous to an Ntuple, which crosses the possible locations within a large container of N candidates with N cells.
The analogy can be extended further. For example:
- If an Xwing in exists for candidate N with respect to columns
- Let M be the number of locations for candidate N that are not yet fixed.
- There exists a fish of size (M-2) with respect to rows
This compares with: If you find a hidden pair in a large container, there exists a naked
(M-2) tuple in that large container.
Swordfish Example
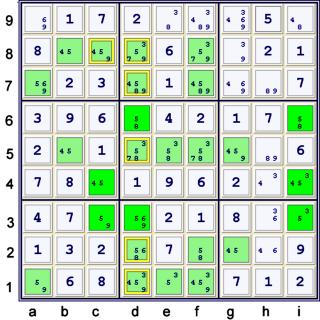
In this example, the possible locations for 5's are highlighted in green. The darker green
cells form the swordfish. In this example, the swordfish is missing 5's at c6,d4.
This is common with swordfish, and does not effect the possible eliminations. In the example,
we have:
- 5's in row 6 limited to d6,i6
- 5's in row 4 limited to c4,i4
- 5's in row 3 limited to c3,d3,i3
- Forbids 5 from: c8,d1,d2,d5,d7,d8
The following table proves the validity of these eliminations:
| | d6=5 | i6=5 |
| c4=5 | | i4=5 |
| c3=5 | d3=5 | i3=5 |
In this table,
- Each row has at least one item that must be true, by examination of the puzzle grid
- Each column has no more than one item that can be true, by the rules of the game (no
need to consult the grid)
Conclusion:
- The table has at least three truths (at each row)
- The table has no more than three truths (at each column)
- Thus, the table has exactly three truths
- Further, each table column has exactly one truth
One can now clearly see that, for example, c8=5 is forbidden. In fact, c125789,d125789,i125789=5 are all forbidden.
The table above could also be called a forbidding matrix. There is more than one
type of such a matrix. Credit for the matrix idea belongs to Andrei Zelevinsky and Bruno Greco (gb). It
should be noted, however, that my presentation of the idea of forbidding matrices
lacks their strict mathematical precision.