A study in Chain Forging: Page 6

Welcome back!

Still awake? This proof still has some teaching left. I am much obliged by your attention. Previous pages of this proof are practically a prerequisite for this page:

1. First Page - Almost Y wing styles as Chain links
2. Second Page - Almost Hidden Pairs as Chain links
3. Third Page - Almost coloring, Almost AIC, Introduction to Appending chains
4. Fourth Page - An introduction to Super Cells
5. Fifth page - An introduction to Appending Chains

The last step on this page is mundane by comparison to the first step. However, the first step is not hard to find, if one truly owns the previous information detailed in this proof.

Rather than bog things down with mundane theories, let us just look at an example.

A Strong link as an appendage, and also the foundation of a super cell

The super cell and its useful outbound links

Almost skyscraper with 5s emanates from the super cell

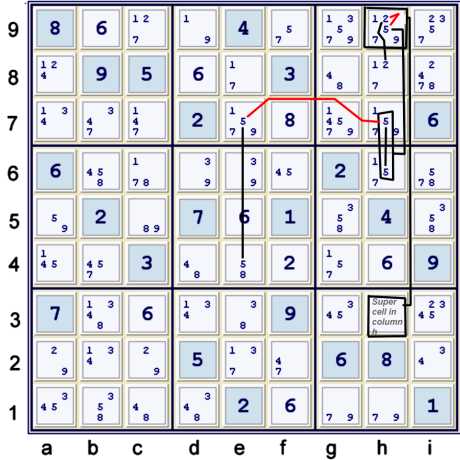
Above, find that I have added the following almost skyscraper with candidate 5:

• h6 *==* h7 -- e7 == e4 => h6 *==* e4

Considering column a and row 5, the rest of the chain is not hard.

Almost skyscraper with 5s links through the super cell with a standard chain

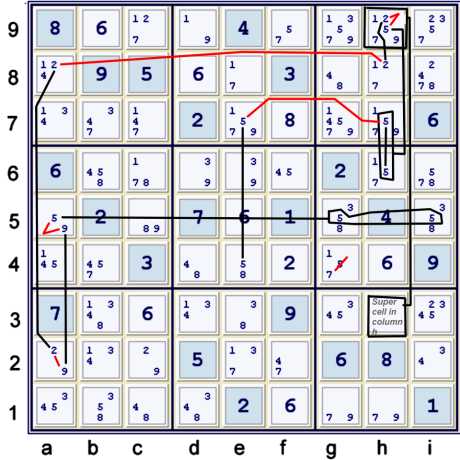
the chain can be written using the super cell:

• {e4=5 == e7=5 -- h7=5 ==₁ h6=5} ==₁ {Super cell h39=5} -- {Super cell h39=2} == h8=2 -- a8=2 == a2=2 -- a2=9 == a5=9 -- a5=5 == gi5=5
  • =>{e4=5 == h6=5} == gi5=5 => g4≠5

The entire chain above can be written without using the super cell as:

• {e4=5 == e7=5 -- h7=5 ==₁ h6=5} == {Hidden pair 35₁ at h39} -- h39=2 == h8=2 -- a8=2 == a2=2 -- a2=9 == a5=9 -- a5=5 == gi5=5
  • =>{e4=5 == h6=5} == gi5=5 => g4≠5

Note that the beauty of this idea, super cells as appendages, is that the 3's are clearly revealed as a bridge between two cells. Thus, one can treat two cells as one, in a limited fashion. Moreover, the entire chain is nothing but an appendage to the base chain idea, a short chain on only candidate 5. Note further that the elimination is valid regardless of how many times 25 actually appear at h39.

As complex as the elimination above may appear, it can be represented by a fairly simple 7x7 pigeonhole matrix, discontinuous type. Using such matrices reveals how the entire elimination presented above can be derived by merely appending.

Appending forbidding matrices to derive strong inferences

The following group of tables are relevant to the elimination being considered. They will progress until the matrix representation aligns with the native puzzle conditions illustrated.

For each of these matrices, the size will be nxn. Each row will be a native strong inference. Each column, except the first column, will have at most one truth (native weak inference). Thus, each matrix will have at least n truths. Columns 2 thru n will contain at most (n-1) truths. Therefor, column 1, the result column, must contain at least one truth (proven strong inference set).

5x5 matrix

The following matrix is an almost matrix relative to the puzzle above.

g5=5	a5=5
	a5=9	a2=9
		a2=2	a8=2
			h8=2	h9=2
h6=5				h9=5

The conclusion of column 1 then is: g5=5 == h6=5. Although this example looks like a continuous chain, and in fact if these native puzzle conditions existed it would be a wrap around chain, the only result this analysis is interested in is: g5=5 == h6=5.

5x5 matrix appended inside a matrix cell

The following matrix is again an almost matrix relative to the puzzle above. It progresses one small step closer to the actual puzzle.

gi5=5	a5=5
	a5=9	a2=9
		a2=2	a8=2
			h8=2	h9=2
h6=5				h9=5

the conclusion of column 1 now is: gi5 == h6=5. We have merely appended the previous matrix.

5x5 matrix appended by adding a matrix row and a matrix column

Again, the following matrix is an almost matrix relative to this puzzle. Here, I append a 5x5 matrix to create a 6x6 matrix.

gi5=5	a5=5
	a5=9	a2=9
		a2=2	a8=2
			h8=2	h9=2
h6=5				h9=5	h7=5
e4=5					e7=5

The conclusion of column 1 has changed significantly, and the matrix is no longer in any way continuous. However, there still exists a target set of possible eliminations. The new conclusions of this almost 6x6 matrix is:{gi5=5,h6=5,e4=5} is a strong inference set. Thus, the target elimination group is now: ghi4≠5.

6x6 matrix appended by adding a matrix row and a matrix column

Finally, the matrix below is no longer an almost matrix. In fact, it is representative of the actual native puzzle conditions.

gi5=5	a5=5
	a5=9	a2=9
		a2=2	a8=2
			h8=2	h9=2		h3=2
h6=5				h9=5	h7=5	h3=5
e4=5					e7=5
				h9=3		h3=3

The conclusions of this 7x7 matrix and the previous 6x6 matrix are the same. Hopefully, the tool of using matrices to illustrate possible ways to append chains is clear. There are many other ways to append chains that have not yet been demonstrated.

One very important note: I do not view matrices as an important solving tool. Rather, they are a great proving tool. As such, they are also a fantastic tool to use to imagine possible theoretical techniques. Of course, one must then construct a logical way to go from matrix to technique observation. That is precisely the reason that I introduced matrices early in the blog, and now have returned to them. I needed to build the observational base!

Now, let us return to the puzzle for one further elimination. This one is relatively easy!

An easy Y wing style that happens to be a wrap-around chain.

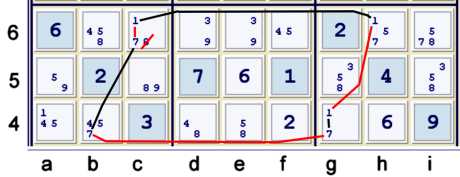
The continuous chain illustrated above has only one useful proven strong link: c6=1 == c6=7. The complete chain can thus be written to clearly indicate the one elimination that is proven:

• c6=1 == g6=1 -- g4=1 == g4=7 -- b4=7 == c6=7 => c6=17 => c6≠8

This concludes the sixth page of this torture. If you are still up for the punishment, dare to click onto page 7 (Almost Y wing Styles again).