The following is an illustrated proof for the
Tough Sudoku of March 29, 2007.
This proof illustrates both the power of using Almost Locked Sets within a
Forbidding Chain, also called an Alternating Inference Chain or
AIC, and using standard forbidding chains.
You may wish to refer to previous blog pages to properly understand
this proof. Links to these pages are found to the right, under Sudoku Techniques.
At many times during this illustration, there are other steps available. It is not the goal
of this page to show every possible step, but rather to illustrate steps that, taken together,
unlock this puzzle.
The information on the following blog pages may be helpful:
The illustrations of forbidding chains used in this proof will share the same key:
- black line = strong inference performed upon a set (strong link)
- red line = weak inference performed upon a set (weak link)
- black containers define either:
- a partioning of a strong set
- the use of an almost locked set
- candidates crossed out in red = candidates proven false
Strong and weak need not be mutually exclusive properties.
Puzzle at start
A few Unique Possibilities are available here:
- b2 = 4% box (hidden singleton in box)
- c6 = 7% box & column
- b8 = 9% box & column
Hidden Pair 28
Quite often, Hidden Pairs are easier to find before entering the possibilities.
Illustrated to the left, d6=2 and f4=8 conspire to force only 28 at e28.
After noting this, f1 = 1% box
Also available at this time, but not illustrated, is the Hidden Pair 89 at h56.
Possibility matrix at 27 cells solved (UP 27)
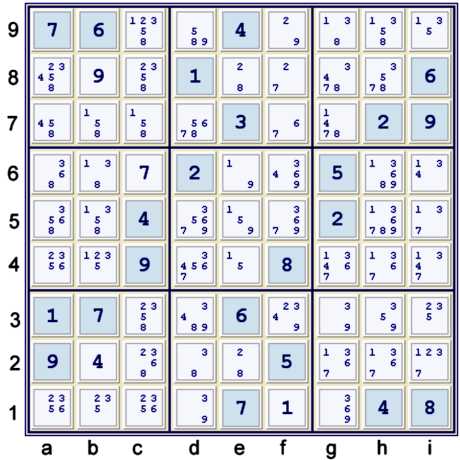
At this point, there are many standard eliminations available. The only one of these that this
proof requires is locked 8s at h56 => h89≠8
The following standard eliminations are not used in this proof, but available at this time:
- Hidden pair 89 at h56 forbids h89=8, h3=9, h5=1367, h6=136
- Locked 1s at c79 forbids b7=1
- Locked 2s at abc1 forbids c23=2
- Locked 4s at i46 forbids g4=4
- Locked 5s at hi3 forbids c3=5
- Locked 5s at e45 forbids d45=5
- Locked 6s at c12 forbids a1=6
- Locked 6s at gh4 forbids ad4=6
- Locked 8s at c23 forbids c789=8
- Locked 9s at e56 forbids d5f56=9
Whew! That is many locked candidate eliminations!
After making these eliminations, if one tries a puzzle mark-up, (explained in some detail
here), one will find that cells d9 and f3 are
strongly indicated as potential forbidding chain pieces - three circles each. In fact, a number
of forbidding chains use these cells. Most of them involve four strong inferences or more.
There are a great number of other forbidding chains also available. All of them that I found
are at least partially indicated by the puzzle marks. I will illustrate only those that I found
to be the most efficient path to solution. Regardless of the path chosen, this is an easy puzzle
from which to extract forbidding chains, or AIC.
Of particular interest, however, are some items not commonly noted on my puzzle marks:
- There are many Almost Locked Set configurations. So many, in fact, that to
list them all could take quite some time!
- The solved cells in box b2 force the 3's in box b2 into an easy grouped argument.
Some may call such a configuration a hinge. This particular hinge is easy to spot
even before the possibilities are entered!
Knocking off a seemingly harmless 3
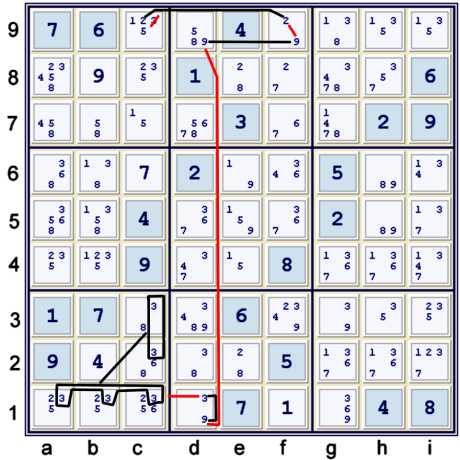
Illustrated above is a standard forbidding chain that uses the hinge with 3s:
- c9=2 == f9=2 -- f9=9 == d9=9 -- d1=9 == d1=3 -- abc1=3 == c23=3 => c9≠3
Oftentimes, the candidate with the most possible locations on the puzzle grid is the easiest one
to attack. Nevertheless, it is often the least valuable one to consider. With this puzzle, though,
the 3's exist in many bivalue cells, such as c3=38, etc. For this reason, they might be important.
Another Locked candidate elimination
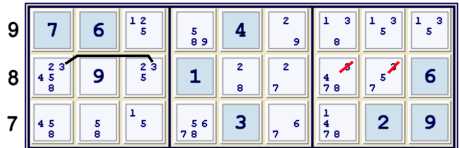
The 3s are now locked in box b8 at cells ac8, forcing gh8 to contain no 3s. Alternatively,
the 3s are locked in row 9 at ghi9, within box h8, eliminating the same 3s.
Almost Hidden Pair 67 used in a chain
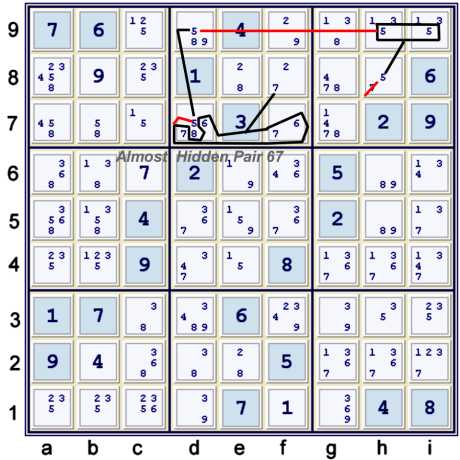
The chain illustrated above uses the Almost Hidden Pair 67 at df7. One could alternatively
use the Almost Locked Naked Triple 2589 at df9 & e8. For me, the Almost Hidden Pair is much easier
to see, but for others it is probably obscure.
The forbidding chain illustrated above can be written as:
- f8=7 == {Hidden pair 67 at df7} -- d7=5 == d9=5 -- hi9=5 == h8=5 => h8≠7
The logic can be described otherwise as follows:
- f8=7 => h8≠7
- f8≠7 => both 67 are locked at df7, thus hidden pair 67 at df7
- d7 limited to only 67 => d7≠5 => d9=5 =>
- hi9 cannot contain 5 => h8=5 => h8≠7
If one were to instead use the almost naked triple, the forbidding chain could be:
- h8=5 == hi9=5 -- d9=5 == {triple 289 at df9,e8} -- f8=2 == f8=7 => h8≠7
The logic could also be described as follows:
- h8=5 => h8≠7
- hi9=5 => d9≠5 => {d9=89, f9=29, e8=28, thus naked triple 289} =>
- f8≠2 => f8=7 => h8≠7
If you are paying attention, one could write either chain differently and use the cell h8=57,
plus the other information, to forbid hi9=5. This is quite common - that one can find many very
similar eliminations. Interestingly enough, though: The elimination of the 5s is available only after
the elimination of the 3, while the 7 elimination is available whether or not one has eliminated
h8=3. It is because I saw this depth 4 elimination that I knew the previous depth 4 elimination of
3 from c9 would be particularly valuable.
After making this elimination, h8=5 and the puzzle becomes a cascade of Unique Possibities to
the end. If one has made all the locked candidate eliminations listed above, one can find naked
singles to the end. If, however, one only makes the steps listed below in my proof, one needs to
find some hidden singles.
Proof
- Start at 22 filled - the given puzzle. Unique Possibilities to 26 filled. (UP 26).
- Hidden pair 28 at e28 forbids e2=1, e8=5 UP 27
- Locked 8s at h56 forbids h89=8
- c9=2 == f9=2 -- f9=9 == d9=9 -- d1=9 == d1=3 -- abc1=3 == c23=3 forbids c9=3
- Locked 3's at ac8 forbids gh8=3
- f8=71 == {hidden pair 671 at df7} -- d7=5 == d9=5 -- hi9=5 == h8=5 forbids h8=7 UP 81
- Sets: 2 + 1 + 4 + 1 + 4 = 12
- Max depth 4, twice
- Rating: 2(.01)+.03 +2(.15) = .35
Not too tough, but at least interesting!
Notes
The value of understanding the concept of Almost Locked Sets is well
recognized across the Sudoku solving community. One can certainly solve this puzzle without using
ALS, but the easiest path, in my opinion, includes using at least one such step.