Solution for Tough Sudoku of August 7, 2009

The following illustrated solution for the moderately difficult Tough Sudoku of August 7, 2009 serves as a reasonably good example of the power of using mixed groups or Sets within or as a Sudoku solving technique. This particular Sudoku solving strategy, tip or trick is sometimes referred to in Sudoku forums as Quantums. This blog has used this strategy numerous times, albeit under the name hybrid.

If this is your first visit to this blog, welcome! Unfortunately, if you are a first time visitor, this page may seem like it is written in a different language. Well, it is!! Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. The earliest posts are at the bottom, and if you have never perused the intricacies of our special coded language here, you may wish to start close to beginning. The list is rather large, so below find a list of links that may be pertinent to this particular puzzle.

• Locked Candidates
• Pairs Triples Quads
• Forbidding Chains 101 The Theory
• Forbidding Chains 102 The Practice
• Unique Rectangles
• Definitions: This page has been recently updated, finally

In some of the illustrations, more than one step is shown at once. This reflects an attempt to shorten the page. However, it may contribute to some confusion. Hopefully, the confusion is managable. Moreover, many easy steps that this solution does not require are not shown, nor taken in the illustrated puzzle positions. Again, this reflects an attempt to shorten the page.

A note: Puzzle solutions which employ Uniqueness techniques, such as this one, I generally call solutions. If Uniqueness is not used, then such a solution is generally called a Proof.

The Puzzle

For those whom do not wish to struggle through the illustrations, I have written the steps taken in this solution at the bottom of the page in sudoku.com.au notation.

Steps 2a & 2b: A Naked Triple and a Locked Candidate

Below, two steps are shown. Step 2a in column g and box h2 is a Naked Triple:

• (NT246)g123 => h1≠26, i2≠4, g489≠246

After step 2a, step 2b, a Locked Candidate, is possible:

• (LC4)de9 => e8de7≠4

Other similar very easy steps are also possible, but not required in this solution.

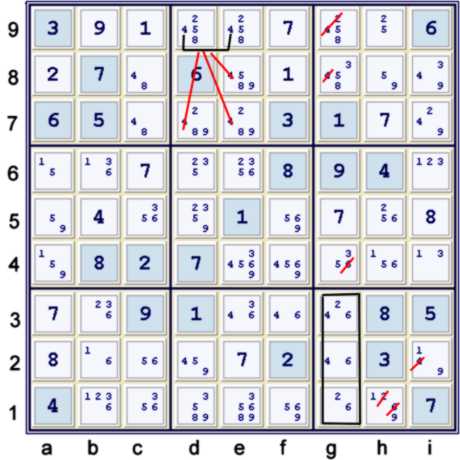
Step 2c: A short Alternating Inference Chain (AIC) previously called Forbidding Chain

Above, a short AIC using four Strong Inference Sets (SIS) is shown. The chain could be written:

• (1=6)b2 - (6)b6 = (6)c5 - (6)h5 = (6-1)h4 = (1)h1
• => b1,i2≠1

This leads to a short cascade of four singles:

1. (9)i2 %cell
2. (9)h8 %box & column
3. (1)h1 %cell & box
4. (1)b2 %row & box, UP 40

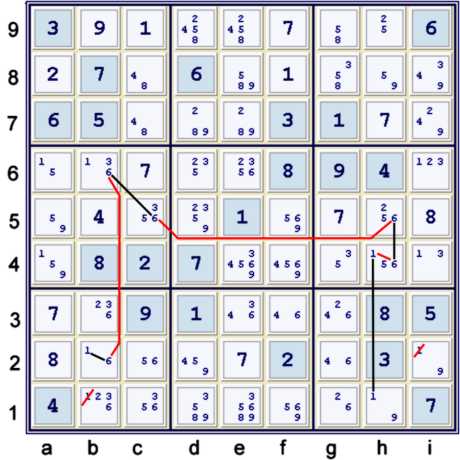
Step 3a: Another short AIC

Below, a rather mundane candidate is eliminated as a set up for the following step. Once again, a short depth 4 AIC is used.

The chain above uses groupings with both candidates (5) and (9). The chain:

• (9)f45 = (9-5)f1 = (5)f45 - (5)de6 = (5)a6 - (5=9)a5 => d5≠9

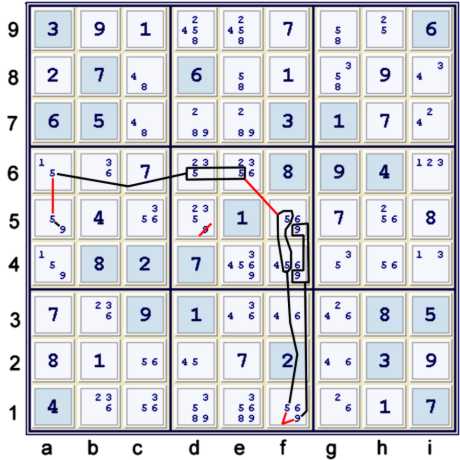
Preamble to step 3b. The derivation of a Quantum set.

Below, the Almost Unique Rectangle (AUR) with candidates (89) at de17 is used to derive a Strong Inference Set (SIS). Such a SIS is sometimes called a Quantum Set. More typically, a Quantum Set is used in conjunction with one or more native set(s) to derive something more interesting. The term Quantum can also be used to describe just about any grouping of items that forms, or almost forms, an atypical representation of a more normal set, such as an ALS (Almost Locked Set). The example below is not nearly that complex.

Step 3b: Two chains folded into one. Uses both Quantum AUR set plus another Quantum Set

Below, one could write two different chains. However, at least some of the information used overlaps, so it is more efficient to simply show one long chain and note the eliminations it causes. The previously AUR SIS is used, plus another atypical grouping. If candidate (5) is contained at f45, then one would have within box e5 the equivalent to a Naked Triple (235) at de56,f45. Candidate (2) is locked within this Almost Quantum Naked Triple at d56, so this quantum set exerts a weak link upon (2)d79. This weak link is one of the endpoints of one of the two chains contained in the larger chain below. The other chain spans from (5)f1 to (5)c2.

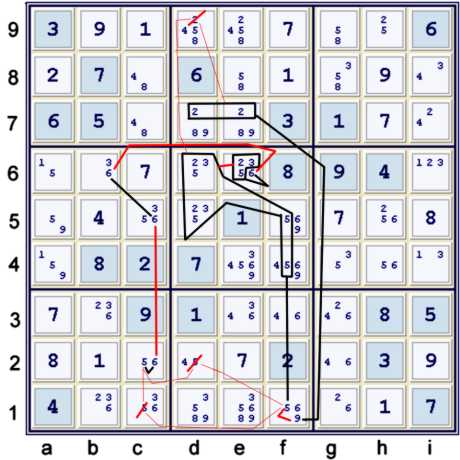
The chain above, given (2)de7=(9)f1 by (AUR89)de17:

• (2)de7 = (9-5)f1 = (QNT235)f45.de56 pause - (235=6)e6 - (6)b6 = (6)c5 - (6=5)c2
• => d9≠2, c1.d2≠5

These eliminations cause a cascade of singles until the puzzle is finished. UP 81.

Solution

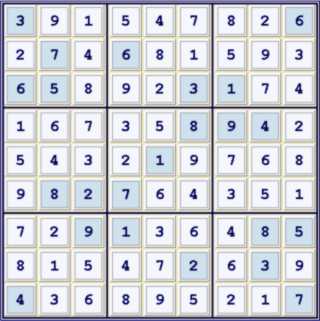
Steps taken in this solution:

• 1) start 23 (HP29)a8b9 => a8<>18,b9<>14 UP 36
• 2a) (NT246)g123 => h1<>26, i2<>4, g489<>246
• 2b) (LC4)de9 => e8de7<>4
• 2c) (1=6)b2 - (6)b6 = (6)c5 - (6)h5 = (6-1)h4 = (1)h1 => i2, b1<>1 UP 40
• 3a) (9)f45 = (9-5)f1 = (5)f45 - (5)de6 = (5)a6 - (5=9)a5 => d4<>9
• 3b) (AUR89)de17 => (2)de7=(9)f1
  • => (2)de7=(9-5)f1 = (QNT532)f45d56 pause - (235=6)e6 - (6)b6 = (6)c5 - (6=5)c2 => d9<>2, c1.d2<>5 UP 81

The following spectrum of SIS considered is of limited relevance:

• Sets: 2+3+1+4+4+10=24.
• Max Depth 10, but can be reduced to 7 splitting step 3b into two steps
• Non-ssts: 3. SSTS refers to Simple Sudoku Technique Set, or something like that
• Rating: .03 + .07 + .01 + .15 + .15 + 10.27 = 10.68
• Alternate rating if step 3b is split: .03+.07+.01+.15+.15+1.27+.63 = 2.33

Digression: Usually, I prefer shorter steps. Thus I might split step 3b into two steps. However, there seems to be a heavy preference towards minimizing the number of steps. In deference to that preference, I have shown that step as one. Clearly, one could often, (perhaps always,) solve a puzzle with one step - although such a step could be large and complex. For example, in this puzzle, one could easily form a large and complex net that uses the same information from all of the steps considered above to produce one step that unlocks the puzzle. That large and ungainly net would be truly ugly, but in some sense quick and to the point. I have no idea where the line lies between minimizing number of steps and minimizing the length and complexity of the individual steps.