Tough of January 30,2008 Page Three

The following is page three of an illustrated proof for the sudoku.com.au tough puzzle of 01/30/08. Page two and page one attempted to finely detail how to find eliminations. This page will continue in similar fashion. This page, and perhaps this entire proof, has a theme: remembering what one has found. A second related, but not quite equivalent, theme is: fully noting possibility matrix changes. Hopefully, this page will serve as a sterling example of how remembering works for me.

Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. I may later list specific pages.

The illustrations of steps shown on this page will share this key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set(s)
• candidates crossed out in red = candidates proven false
• boxes highlight some groups

Please be aware that, for me, strong and weak need not be mutually exclusive properties.

Mark-Up

After each elimination, including cell solutions, I find it helpful to manually update my puzzle mark-up. This forces me to be aware of what has changed. Thus, newly stronger strong inference sets are noted. Often, I spend some time examining those newly stronger (meaning more restricted) sis.

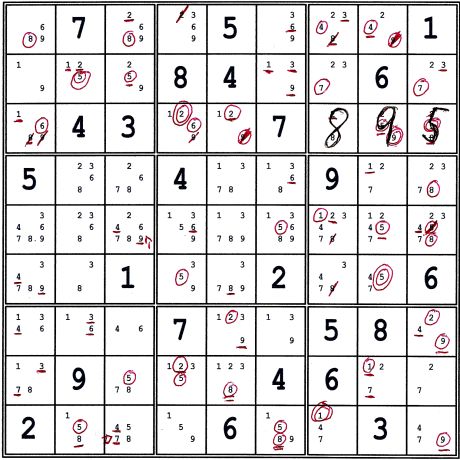
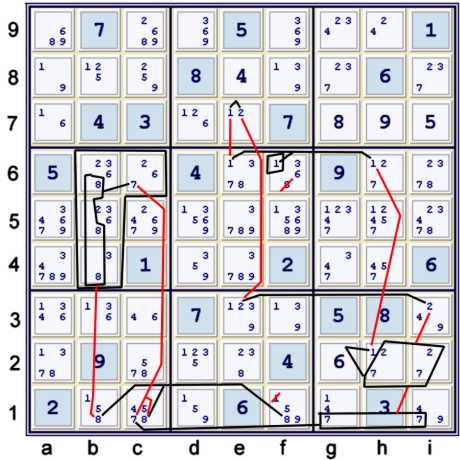
the mark-up above includes the result of step 3a: Locked 2s de7 => d9 ≠2. Note that candidate 8 required multiple updates. (8)ac9 both became circled. (8)e4 received an underline because of (8)e4=(8)ab4. The next step is the immediate result of those updates.

Steps 3a & 3b

Below, the Locked 2's elimination is graphed. Also, two different ways to achieve the same eliminations with candidate 8 are shown.

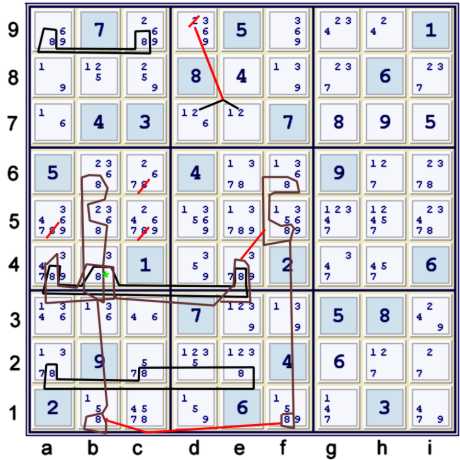
Using only candidate 8, both of the following justify a5,d56≠8:

1. b456=b1-f1=f56-e4=ab4
2. b4=[row swordfish ace2, ae4, ac9] - a finned swordfish.

The latter requires both stronger 8s in row 9 and row 4. The one I found first required only the stronger 8s in row 4. Thus, although the finned swordfish is more pattern-like, the simple chain listed first is in my mind easier to spot given:

• a single candidate elimination search has been previously conducted.
• the underlined 8's in my puzzle mark-up at b1,f1,e4

It has been argued by others that finding such groupings is beyond typical human pattern recognition. This is not only silly, but clearly only true if one chooses not to ever look for them.

Finally, note the exquisite symmetry between the two chains making the same elimination: both have the same appendage that prevents a continuous, or wrap around situation: (8)b4. Furthermore, without (8)b4, both would have precisely the same targets. Somewhere, lurking within this symmetrical relationship lies a deep uniqueness of solution argument. But, I digress.

Step 3c

Below, the new Bivalue (1=2)e7 plays an important role. Some may prefer two chains.

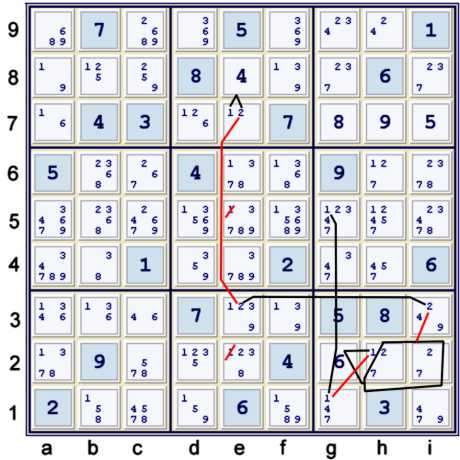
The key to this one is the ALS (127)hi2. Thus, in that box we have the equivalent of the additional sis: (1=7)hi2 and (1=2)hi2. (1=2)hi2 is the most important in this deduction, as the new (1=2) at e7 forms the equivalent of a Y wing style:

• (1=2)e7-(2)e3=(2)i3-(2=1)hi2

The chain, as shown above, also recognizes the continuation: (1)g1=(1)g5. Thus, the entire chain written more formally:

• (1=2)e7-(2)e3=(2)i3-(pair27)hi2=(1)h2-(1)g1=(1)g5 => e25≠1

Thus, the key to this one, for me, is not only recognizing the sis (1=2)hi2 created by the ALS(127)hi2, but more importantly realising that the new sis, (1=2)e7, and the old sis, (1=2)hi2, can be easily linked.

Step 3d Prelude 1

Below, step 3c revealed an Almost Wrap Around Chain that is readily apparent if one looks for such animals. Moreover, note the overlap with the previous step.

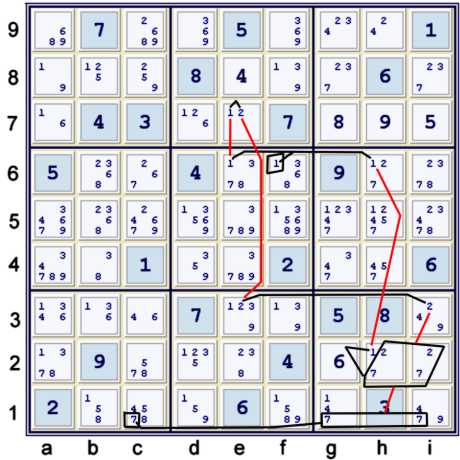
Finding Almost Wrap-Around Chains is usually worth the effort. This is because such an almost chain has mulitple weak links emanating from it, or alternatively, almost proves multiple sis. Recall that with a standard wrap around chain all the weak links are proven strong. Thus, above,

• (1)f6=[wrap around chain: (1=2)e7-(2)e3=(2)i3-(pair27)hi2=(1)h2-(1)h6=(1)e6]
• => (1)f6=sis list[(1)e67, (2)e37, (7)hi2, (2)i3hi2, (1)h26]

That is a lot of potential bang for the buck. In my head, I recognize (7)gi1=(7)c1 because (7)c1 is underlined in the puzzle mark-up. Thus, to remember this chain snippet, I note in the margin of my puzzle mark-up only: (1)f6=(7)c1. Since step 3c used four of the same sis, this shorthand is quite sufficient.

Step 3d Prelude 2

Step 3d - Linked AAIC

Below, I graph Prelude 1 and Prelude 2 together. The deduced chain, therefor:

• (1)*f6=[(1)*e6=(1)*h6-(1)h2=(pair27)hi2-(2)i3=(2)e3-(2=1)e7]-(7)gi1
• =(7)c1-[[(7)c6&(-8)**c1]=(ht479)a45c5-(8)a4=(8)b465-(8)**b1]=(8)**f1
• => (1)f6=(8)f1 => f1<>1, f6<>8 native depth 11

For reference, and to illustrate how a Mixed Block Matrix handles such an animal, one can study the matrix below. Note that there are two Symmetric Pigeonhole Matrix blocks, both of which are indicated by bold characters. Please remember: the finding of such an animal can be done in at least two distinct, but formally related manners:

1. Linking AIC chain snippets, as fully illustrated above
2. Counting potential matrix rows versus columns, as described in previous blog pages

1r6	f6	e6	h6
e7		1		2
2r3				e3	i3
i2					2	7
h2			1		2	7
7r1						gi1	c1
c6							7	2	6
b6								2	6	3	8
b5								2	6	3	8
b4										3	8
8r1	f1						c1				b1

Not shown: Afer making these eliminations,

• Step 3e: (Hidden Pair 58)f15 => f1≠9 & f5≠1369

This requires a refresh of my puzzle mark-up, as now (9)d1=(9)i1, (6)d5=(6)f6, (8)f1=(8)f5. Circling the (6) at f6 and (6) at d5 provided an essential clue for the next cascaded step.

Step 3f Prelude

Below,

• (6)d5=[(6)f6-(1)f6=(7)c1see previous step]-(67)c6=(2)c6
• => (6)d5=(2)c6.

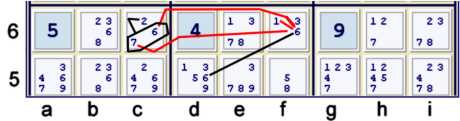
At this point, I note in my puzzle mark-up both 1 & 2 underlined at b8. These serve as a clue for a helpful continuation to (6)d5=(2)c6.

Step 3f

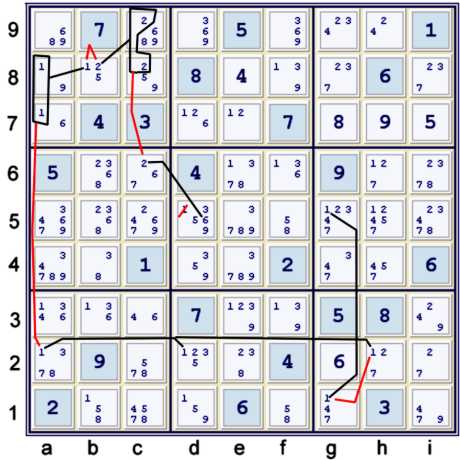
Above, to make the graphing easier, I have replaced (1)b8=(1)b13 with (1)b8=(1)a78. Also, (2)b8=(2)b56 is replaced with (2)c89=(2)b8. However, the underlined (12)b8 meant the latter. The chain now reads:

• (6)d5=(2)c6-(2)c89=(2-1)b8=(1)a78-(1)a2= [(1) d2=h2-g1=g5]
• => d5≠1
• => circle (1)e6,(1)f6 => (not shown)
• step 3g Locked 1s ef6 => h6≠1

If one cares to, one can find a chain, depth 9, that replicates step 3f. I generally do this, as it helps me to understand other things about the puzzle. I guess one could call that activity puzzle study. I find it often helpful. Here, my notes say D9 poss, meaning independent Depth 9 chain possible to achieve the same elimination. Independent means that it requires no knowledge of any previous steps. But, again I digress!

For reference and illustration purposes, below find an 8x8 Triangular Matrix that is actually depth 9. In bold, note that I treat the ALS(127)hi2 as a single Boolean:(1)h2=(pair27)hi2. This can be done freely without any loss of generality.

1g	g5	g1
1r2	d2	h2	a2
1b			b13	b8
2b				b8	b56
hi2		1				p27
7r1						gi1	c1
c6					2		7	6
6Bx5	d5							f6

Alternate Step 3f - simple TM

This content has been added later. First, let me apologize. Oftentimes, I find many ways to justify the same elimination. What follows is another way to achieve step 3f. One could write this alternative as an AIC, but it is a bit messy. The idea has some overlap with the previous two manners shown to achieve d5≠1:

• [(1):g5=g1-h2=*d2]=*(1)a2-[(1)b13=(1-2)b8=(2)b56-(2=7)**c6-(7)a45=(7)a2]=(6)**c6-(6)f6=(6)d5
• => sis[(1)g5,(1)d2,(6)d5] => d5≠1

The key to finding this one is the confluence of underlines:

(1)b8, (2)b8, (7)a2

yielding [(1)d2=(1)h2]=(6)c6 when combined with (267)c6

As a TM, depth 7:

1g	g5	g1
1r2	d2	h2	a2
1b			b13	b8
2b				b8	b56
7a			a2			a45
c6					2	7	6
6B5	d5						f6

Step 3h - ALS again.

This proof continues on Page four. Significant progress has been made.