Almost Locked Sets Proof for March 17, 2007

The following is an illustrated proof for the Tough Sudoku of March 17, 2007. This proof illustrates the power of using Almost Locked Sets within a Forbidding Chain, also called an Alternating Inference Chain or AIC.

You may need to refer to previous blog pages to understand this proof. Links to these pages are found to the right, under Sudoku Techniques.

At many times during this illustration, there are other steps available. It is not the goal of this page to show every possible step, but rather to illustrate steps that, taken together, unlock this puzzle.

The information on the following blog pages is required to understand this page:

• Locked Candidates
• Pairs, Triples, Quads.
• Forbidding Chains 101 The Theory
• Almost Locked Sets
• Definitions: If a term is used on this page that you do not understand, the definition is likely here!

The illustrations of forbidding chains used in this proof will share the same key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set
• candidates crossed out in red = candidates proven false

Strong and weak need not be mutually exclusive properties.

Puzzle at start

Locked candidate with 5s

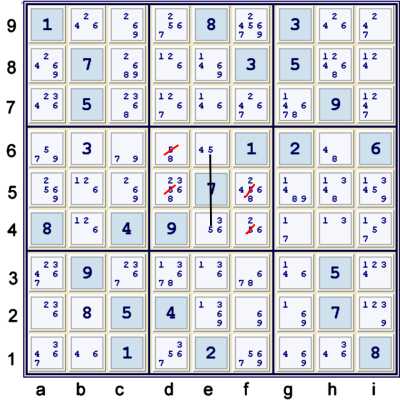
Illustrated above, candidate 5 is locked within column e at e46. Since e46 is entirely within box e5, 5 outside of column e but within box e5 would yield no 5s in column e. Thus, the 5s indicated are eliminated. Clearly, these eliminations lead to a few more solved cells, starting with d6 = 8% cell.

Almost Naked Triple

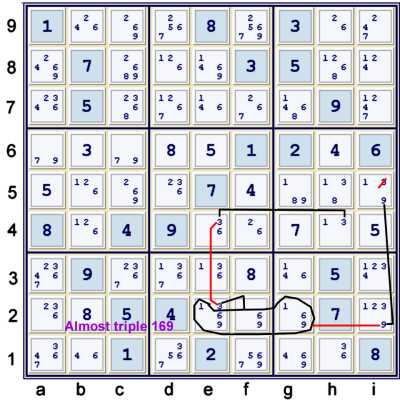
The short chain above uses the Almost triple 169 at efg2 within a chain:

• h4=3 == e4=3 -- e2=3 ==₁ {triple 169 at e2₁f2g2} -- i2=9 == i5=9 => i5≠3

The idea here is that both e24 cannot be 3.

• If e4≠3 then h4=3 => i5≠3
• If e2≠3 then efg2 contains triple 169 => i2≠9 => i5=9 => i5≠3

This is typical fare for using a naked Almost Locked Set within a forbidding chain, or AIC.

Alternate step: Almost Hidden Pair

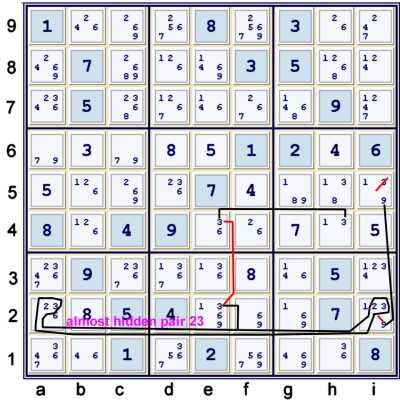
As noted previously in this blog, Hidden sets and Naked sets coexist. This is also usually the case with Almost Hidden Sets and Almost Naked Sets. Illustrated above:

• h4=3 == e4=3 -- e2=3 ==₁ {Hidden pair 23₁ at ai2} -- i2=9 == i5=9 => i5≠3

Again, the idea here is that both e24 cannot be 3:

• If e4≠3 then h4=3 => i5≠3
• If e2≠3 then ai2 contains Hidden Pair 23 => i2≠9 => i5=9 => i5≠3

This clearly illustrates the co-existence of conditional Naked and Hidden sets.

Most solvers at other sites prefer the first ALS chain, using the naked triple. I happen to prefer the latter ALS chain, using the hidden pair.

Another View of the same elimination

Another way to view the same elimination can be found. I will not illustrate this one graphically, but instead will just present the chain:

• {fc on 3s: h4 == e4 -- e2 ==₁ i2} ==₁ a2=3 -- a2=2 == i2=2 -- i2=9 == i5=9 => i5≠3

This representation uses an Almost Coloring technique. It relies upon the fact that a2=3 or a2≠3.

• If a2=3 => i2=2 => i5=9 =>i5≠3
• If a2≠3 => coloring on 3s(side ways skyscraper at eh4,ei2) => i5≠3

There is some value in understanding all three ways to look at this elimination. If nothing else, one has many potential ways to find the elimination.

Locked Candidate with 3s

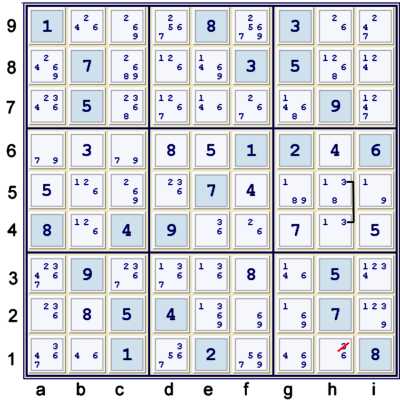
Above, the newly Locked 3s at h45 (or, if you prefer, i23) prove h1≠3. This elimination starts a cascade of Unique Possibilities to the end.

Solution

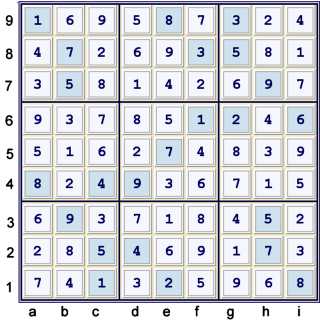
Proof

1. Start at 23 filled - the given puzzle. Unique Possibilities to 25 filled. (UP 25).
2. Locked 5's at e46 forbids d56f45=5 UP 33
3. 1. h4=3 == e4=3 -- e2=3 =={hidden pair 23 at ai2} -- i2=9 == i5=9 forbids i5=3
   2. Locked 3s at i23 forbids h1=3 UP 81

• Sets:1 + 4 + 1 = 6
• Max depth 4 at step 3.1
• Rating: .01 + .15 + .01 = .17

Using Almost Locked Sets makes this puzzle Almost trivial!