Easy Proof of Tough Sudoku March 31,2008

The following illustrated proof for the Tough Sudoku of March 31, 2008 employs a small group of Sudoku techniques, tips and tricks: Hidden Pairs, Hidden Triplet, Locked Candidates, and Alternating Inference Chains.

Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. This list is getting long, so specifically, one may want to refer to the following previous blog pages:

• Locked Candidates
• Pairs, Triples, Quads
• Forbidding Chains 101 The Theory
• Definitions: Most terms used on this page have a defintion somewhere on the defintions page - although an update is long overdue.

Many steps not illustrated are possible. To show every possible step is, well, just overkill. However, this page illustrates sufficient deduced elimination steps to both solve the puzzle, and also to prove a unique solution.

The illustrations of forbidding chains, also called Alternating Inference Chains (AIC), shown below will share this key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set(s)
• candidates crossed out in red = candidates proven false

Please be aware that, for me, strong and weak need not be mutually exclusive properties.

Style Change

Previously, I had abandoned using the chessboard algebraic notation in favor of the more common rc notation. However, since many people have begun again to post proofs on the tough pages, I am hereby returning to algebraic notation. I will retain some of the Eureka-like qualities of writing AICs, though. Hopefully, this does not create too much confusion for those from either group. Illustrations will include the cell descriptive labels to help with interpretation.

The Puzzle

Steps 1b & 1c - Locked Candidates 5 & 9

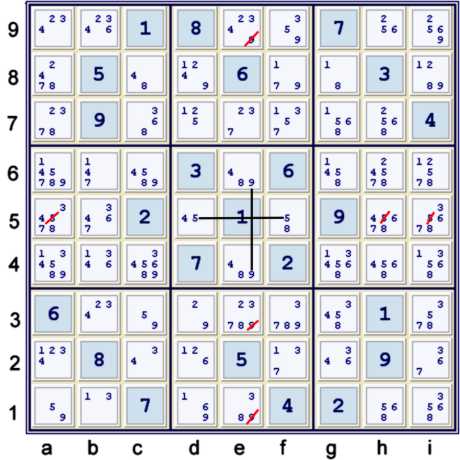
Above, two easy steps are illustrated:

• step 1b Locked candidate 5 at df5 in box e5 (box 5) => ahi5≠5
• step 1c Locked candidate 9 at eh6 in box e5 (box 5) => e139≠9

The symmetry of these eliminations, plus the already found Hidden Pair 59 in step 1a caused me to muse for a bit about Uniqueness of solution with this puzzle. What follows immediately below is basically a digression, but it helps to reveal how I quickly came to solve this puzzle.

A uniqueness digression

Once upon a time, I stayed away from Uniqueness of Solution as a solving technique. Eventually, I changed my mind. The main reason for changing my mind follows:

• Every puzzle that I have tried to solve over the last few years had exactly one solution
• My mind processes much about pattern recognition without my awareness
• The process of knowing where to look is filtered by my experience
• => My experience is inescapably prejudiced by uniqueness of solution
• => I am using uniqueness of solution, whether I want to or not
• If I cannot avoid using uniqueness of solution behind the scenes in my mind, I may as well use it explicitly.

Puzzle Mark-up

Below, find a typical puzzle Mark-up. Note that I include the eliminations from three more locked candidate steps. These steps are not required to solve this puzzle. However, they did help me locate where to look.

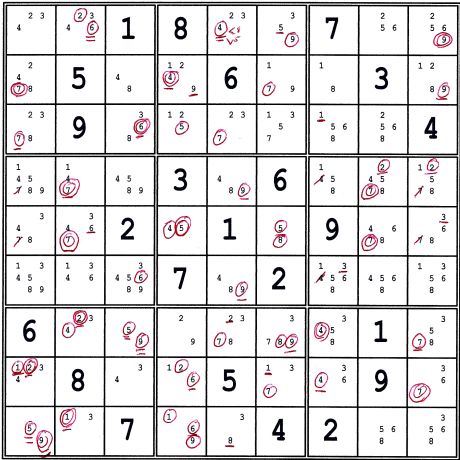
While making the puzzle marks, I thought about a possible MUGgish deduction. Also, one could have viewed it as a BUG. However, what I found with very little thought was a long chain involving an Almost Unique Rectangle. Although I do not use the following chain in my solution, it quickly let me see how to proceed with this puzzle. There were several other chains that I uncovered during the process of marking the puzzle. Typically, a small amount of time investigating potential chains during the puzzle mark-up phase pays significant dividends later. The puzzle becomes burned into my brain. I can then manipulate chains with much greater ease. Here is what I found:

• (Triplet 458)adf5=(3)a5-(3)a79=(hidden pair 36)b9c7-(2)b9=(2)b3-(2=9)d3-(9)c3=(Xwing 9)ce46
• With an Xwing contained in two boxes, there may exist a hidden AUR deduction. Here I continued:
• -(Xwing 8)ce46=[(8)af5=(hidden triplet 589)a146-(1)a46=(1-2)a2.....]

I did not make any eliminations, nor reach any certain conclusions. However, I exposed some potential puzzle weaknesses. This is often the case with musings. Now, the finished puzzle mark-up combined with that chain going nowhere focused my search. Specically, I know now that (1)box b2 determination will significantly unlock the puzzle. Fortunately, this is easily resolved. In fact, I did not need to complete the puzzle mark-up - but decided to do so for illustration purposes.

Do not worry if you cannot follow my logic above. It is the result of solving far too many Sudokus. What follows below can be located without the Uniqueness Digression. However, I wanted to include the digression, as often I am asked to explain how to determine where to look. The answer is not simple, nor always the same. However, in a general fashion it can be said to be exploring chain snippets.

Step 1d - A Hidden Y Wing Style

Y wing style merely refers to any chain that contains exactly three strong inferences. The logic below is exactly like a standard Y wing, except that in this case only hidden strengths are considered. The mark-up exposes hidden strengths, and their intersections. In practice, I see from the mark-up (1)b1%chain.

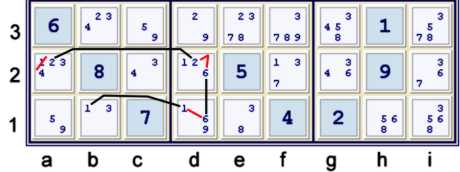
Above, find:

• (2)a2=(2-6)d2=(6-1)d1=(1)b1
• => a2≠1

Thus, one cell is solved: (1)b1 %box.

step 2a - Hidden Triple 159

step 2b - An easy depth 4 chain.

Step 3 - another easy depth 4 AIC

After solving the cells indicated above, the following new information led me to find the chain below:

• New Bivalue (2=7)e7
• New Bilocation (4)a2=(4)a8

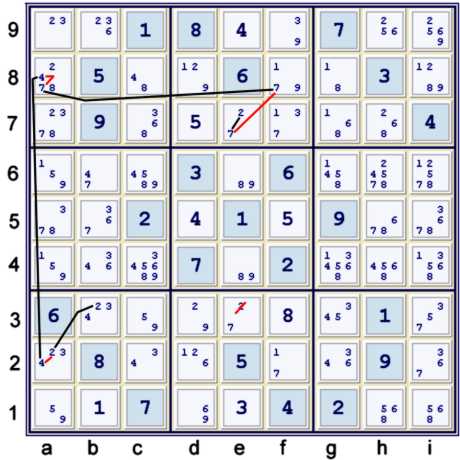
Above, find:

• (2)b3=(2-4)a2=(4-7)a8=(7)f8-(7=2)e7
• => e3≠2

This causes a cascade of mostly naked singles to puzzle completion.

Solution

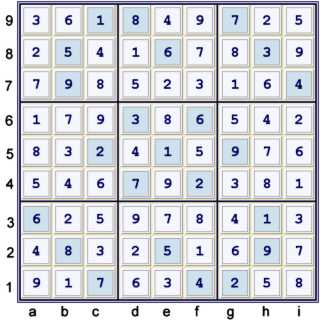
Below, find the rating data that I think is still relevant for easy tough puzzles:

• Strong inference sets considered: 2+1+1+3+4+4 = 15
• Maximum depth: 4. Twice.
• Rating: .42

A rating of .42, in my experience, means a pleasurable puzzle that will not consume too much time. However, it is also challenging enough to preclude boredom.