The following is page four, the final page, of an illustrated solution for the
Tough Sudoku of November 28, 2007. Their are no truly
difficult steps on this page.
Page One of this solution was primarily about the use
of an Almost Unique Rectangle in a chain.
Page Two of this solution included one complex step linking
several disparite types of Almost AICs.
Page Three of this solution also included one complex step
linking two Y Wing Styles. There are many ways to finish this puzzle. One path is illustrated below.
Previous blog pages may be helpful. Links to these pages are found to the right, under
Sudoku Techniques.
Step 5a - Locked candidate 9
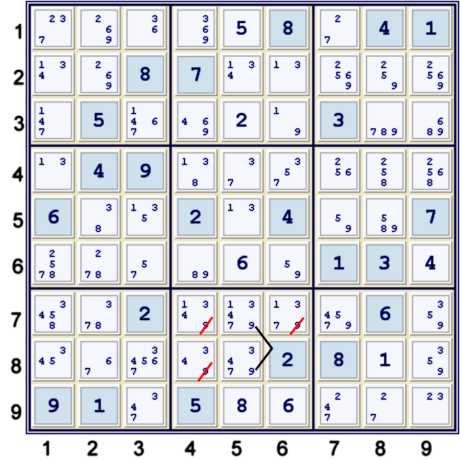
Above, candidate 9 is limited to column 5 within box 8, thus it cannot exist outside of column 5 within box 8.
Step 5b - a short chain using an Almost Naked Pair
On the left,
- (3=4)r8c4-(4)r3c4=(4)r2c5-(4=pair13)r24c1
- => r8c1≠3
Step 5c - a longer chain that could be viewed as two chains
On the left,
- (8)r7c1=(8)r7c2-(8=3)r5c2-(3=1)r4c1-(1)r5c3=(1-4)r3c3
- =(4)r23c1 => r7c1≠4
- continue chain: -(4=5)r8c1 => r7c1≠5
Once one has done the work of finding the depth 5 chain forbidding (4) from r7c1, adding the
strong inference set (sis) (4=5)r8c1 is very little extra work to eliminate (5) from r7c1. One might
alternatively find:
- (HP38)r7c12=(3)r89c3-(3=6)r1c3-(6=pair29)r12c2-(2)r1c1=(2-8)r6c1=(8)r7c1
- => r7c1 limited to (38) => r7c1≠45
Again, there are
always multiple ways to justify an elimination.
Step 5d - Locked candidate 5
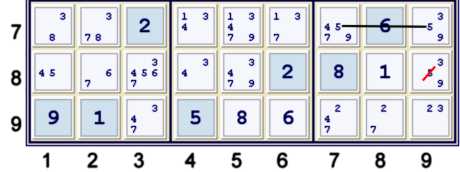
Above, candidate 5 is limited to row 7 within box 9, thus it cannot exist outside of row 7 within box 9.
Step 5e - Hidden Pair 59 - Hidden Pair 54 used in a chain
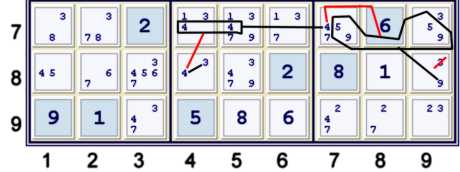
The newly stronger 5's in box 9 row 7 form a super cell such that only one other candidate can fit into r7c79. Thus,
- (9)r8c9=(HP59-HP54)r7c79=(4)r7c45-(4=3)r8c4 => r8c9≠3
- => (9)r8c9 %cell
- => (9)r7c5 %box (& %row, & %column)
- => UP 31
Step 6 - Skyscraper with candidate 1
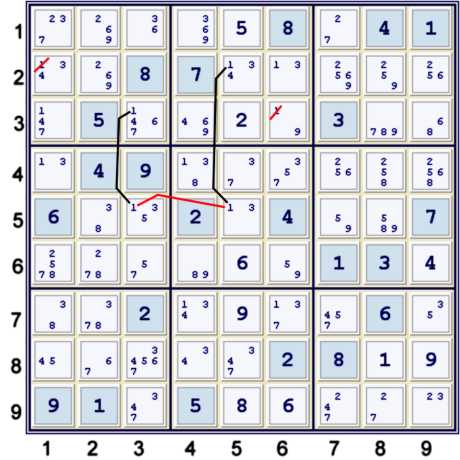
The last step made candidate 1 stronger in column 5, revealing a simple coloring chain with candidate 1
that finishes the puzzle:
- (1): r2c5=r5c5-r5c3=r3c3 => r2c1,r3c6≠1
- => (9)r3c6 %cell
- => (5)r6c6 %cell
- => (5)r5c3 %box
- => %cell (naked singles) to end => UP 81
Solution
Notes
- Step 4b on page two is by far the most difficult step of this solution. It is depth 9, which is also the
deepest step used in this solution.
- Step 2d on page one used an Almost Unique Rectangle. I think that step is the primary puzzle breaker.
- Step 4g on page three employed linked Y Wing Styles. I found that step to be the most fun.
All of the steps can be reduced to counting. Counting certainly works as an idea that catches everything. However, it
seems to provide scant insight into how one might break a puzzle down into managable pieces. I may change my mind about that
evaluation.....
The proof that counting can catch everything is trivial. Counting allows one to consider any arbitrary sis
at any time. It also insures that each weak inference emanating from any arbitrary sis can be considered. Thus, there exists
no sudoku axiom that counting cannot consider - except perhaps Uniqueness. However, uniqueness of solution is never required
to solve a puzzle. It merely provides a convenient short-cut, at times.
Of course, this is nothing earth-shattering. It is not even sudoku world shattering! It really is only a brute force
method of allowing complete axiomatic coverage. At this time, (for truly difficult puzzles), I primarily locate potential
puzzle weaknesses using snippets of known techniques. Sans such devices for deciding where to look, I am not sure that
counting saves time. In fact, it may just be too general to be of much use in deciding where to look.