A Solving Path for July 15, 2010 Tough

The Tough Sudoku of July 15, 2010 is ranked 9.0 by Sudoku Explainer, but is not terribly difficult. One step which I choose to use to solve this puzzle lightly hits upon the theme of the previous blog post: the sudoku tip, trick or technique of using Almost Continuous Loops.

If this is your first visit to this blog, welcome! Unfortunately, if you are a first time visitor, this page may seem like it is written in a different language. Well, it is!! Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. The earliest posts are at the bottom, and if you have never perused the intricacies of our special coded language here, you may wish to start close to beginning. The list is rather large, but you may have some hope of understanding this page if you visit the Definitions page.

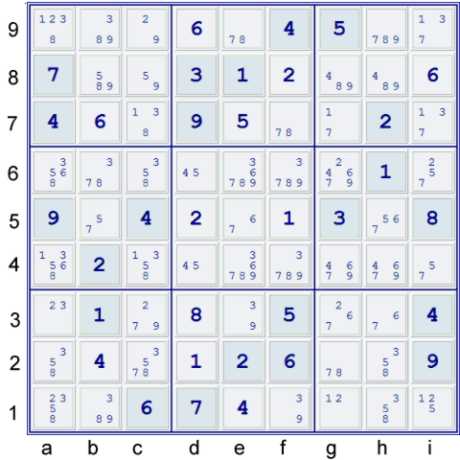
The Puzzle Including Possibilities (Pencil Marks)

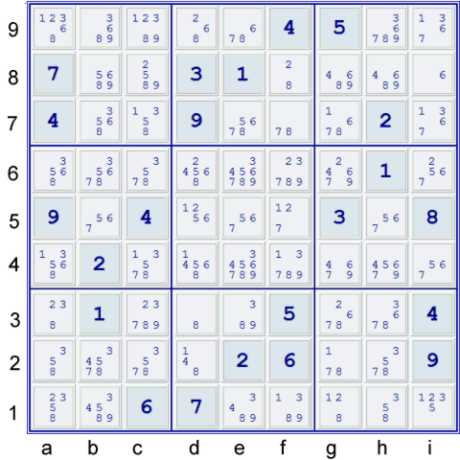
Above, find the puzzle as given with the Possibility Matrix already filled in. A small handful of easy steps are available:

• (6)i8 % cell - a single in the cell i8
• (8)d3 % cell
• (5)e7 % Box - a single in Box e8
• (6)b7 % Row - UP 26 (Unique Possibilites to 26 solved cells)
• Hidden Pair(12) - HP(12)df5 => df4≠1, df6≠2, d5≠56, f5≠7

This brings the puzzle to the state below.

Puzzle after easy steps

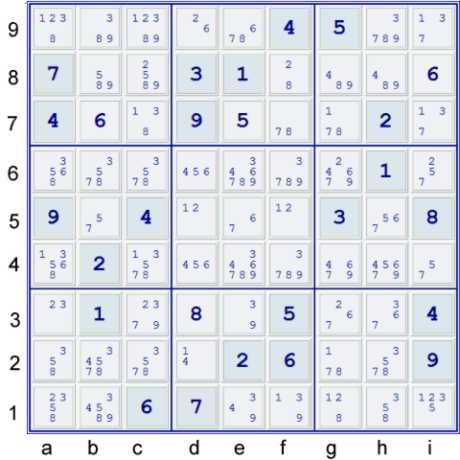
A mundane step - step 2)

Although this puzzle has a number of interesting possible first moves, the following unremarkable step seems to be a good way to start.

• (2)f8 = (2-6)d9 = e9 - (6=7)e5 - (7=5)b5 - b8 = (5)c8
• => c8≠2
• => some singles until UP 33
• LC(7)c23 => c46≠7

Digressive Note: here one can likely kill the puzzle quickly with just one or two complex steps. Most puzzles can be quickly dispatched with just a small handful of moves. My preference is to look for pattern-like moves whenever possible. The pattern-like moves are rarely the most efficient. They are often fairly elegant, however. Of course, elegance is subjective. Some may prefer the quick puzzle kill regardless of the means used to accomplish the feat. If that is your preference, this blog will likely be faintly satisfying.

A Continuous Loop - step 3a)

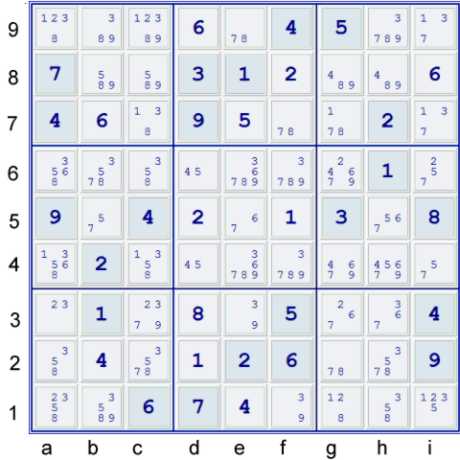
Continuous Loops are, IMO, the most beautiful of steps in Sudoku. In many ways, the entire idea of building a single solution puzzle is interwoven tightly with the concept of avoiding too many overlapping continuous loops whilst leaving just enough room to still have at least one solution. But again, I am digressing..... The loop I found involves just three sets of Strong Inference Sets (SIS):

1. Column c - one can consider
   • candidates (279) in this column
   • or cells c24678 - I will arbitrarily use these SIS in the presentation
2. (5) in rows 5 & 8
3. Box h2 - one can consider
   • candidates (1267) in this Box
   • or cells g2, h1, h2 - I will arbitrarily use these SIS in the presentation

Here is the step: Key: Naked Quad (NQ), Naked Triple (NT), Loop => every SIS considered can be a start point

`
• (7=NQ1358)c2467 - (5)c8 = b8 - b5 = (5)h5 - (NT538=7)h1hg2 Loop
• => c9≠1, c89≠8, c39≠3, b16,h4≠5, g1≠8, h39,i1≠3

A nice little step that yields 12 eliminations. More importantly, it establishes for the solver a group of possibilities which must be True/False together as a group. Hence, this group will likely

• go a long way towards solving the puzzle if any one member can be solved.
• act as a powerful analysis tool for the remainder of the puzzle
• all of the above

Even if one chooses to not execute this step, the awareness that this group of SIS will solve into just one of two groups will likely be helpful.

A Practically New Puzzle - steps 3b) & 3c)

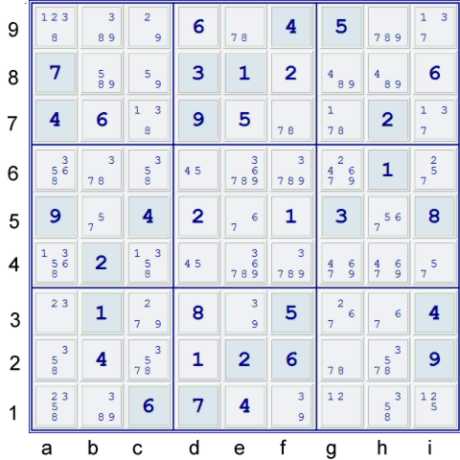
This next step is relatively easy. Steps like this one can pop out into the "obvious" realm given enough practice. It is useful to see it in a few different representations. Three related ways to view this step are given below (1 - a fancy name, 2 - a naked set chain, 3 - a mixed hidden and naked sets chain):

1. ALS xz rc(3) => NT(578)acg2 = NT(267)agh3 => h2≠7
   • ALS xz rc(3) means Almost Locked Sets with restricted common (3)
   • it is based upon the fact that (3) cannot exist at both ac2,a3.
   • One could ignore the fancy names and write:
2. NT(578)acg2 = (3)ac2 - (3=2)a3 - (2)g3 = NP(67)gh3 => h2≠7
3. (3)h2 = ac2 - (3=2)a3 - (2)g3 = HP(21-15)gi1 = HP(53)h12 => h2≠78

Note that regardless of how one views it, the overall relationship of the candidates with each other within Box h2 is reused from the previous step.

After that step, this other step also takes advantage of the overlap with step 3a:

• (8=7)g2 - (7=NQ1358)c2467 - (5=NT948)cgh8 => g7≠8

This finally brings the puzzle to the point where the step which motivated me to create this blog page is most readily available.

Step 3d) A succinct usage of Almost Locked Candidate Base Sets

Huh? Again, I ban myself from ever actually naming anything - for which my children are quite grateful! Below, An Almost Continuous Loop, or Network, considering only candidate (7) can break the puzzle open. It can be viewed as having the XWing concept as the base.

Here is the step:

• (7=NT835)g2h12 - (5)h5 = (5-7)b5 = (7)FinnedSwordFish bfi467 Fin i9
• => g7≠7
• => UP 81 - Singles, naked and/or hidden, until finished

Much like ALS's, here one can consider Almost Locked Candidate (7) to see that: in columns bfi, r46 can contain at most two truths - An Almost XWing, if one prefers - thus SIS (7)[b5, f7, i79]. This makes the chaining almost trivial:

• (7)f7i79 = (7-5)b5 = (5)h5 - (5=NP38)h12 - (8=7)g2

Again, note how the original Continuous Loop from step 3a helps provide a map of SIS to reuse in these later steps. IMO, puzzles which fall apart based upon such reused chain fragments are easier than those which require one to find entirely new SIS groups for most steps.

The steps from above all in one place

1. Start 22 UP 26; HP(12)df5 => df4≠1,df6≠2, d5≠56, f5≠7
2. (2)f8 = (2-6)d9 = e9 - (6=7)e5 - (7=5)b5 - b8 = (5)c8 => c8≠2; UP 33; LC(7)c23 => c46≠7
3. 1. (7=NQ1358)c2467 - (5)c8 = b8 - b5 = (5)h5 - (NT538=7)h1hg2 loop => c389≠138; b16,h4≠5; g1≠8; h39,i1≠3
   2. ALS xz rc(3) => NT(578)acg2 = NT(267)agh3 => h2≠7
   3. (8=7)g2 - (7=NQ1358)c2467 - (5=NT948)cgh8 => g7≠8
   4. (7=NT835)g2h12 - h5 = (5-7)b5 = (7)FSFbfi467 Fin i9 => g7≠7; UP 81

For step minimizers, here is a slightly different path:

1. Start 22 UP 26; HP(12)df5 => df4≠1,df6≠2, d5≠56, f5≠7
2. (2)f8 = (2-6)d9 = e9 - (6=7)e5 - (7=5)b5 - b8 = (5)c8 => c8≠2; UP 33; LC(7)c23 => c46≠7
3. 1. (8=7)g2 - (7=NQ1358)c2467 - (58=NT948)cgh8 => g7≠8
   2. (7=8)g2 - (8*)h1 = [(5*=3*)h1 - f1 = e3 - (3=2)a3 - g3 = HP(21-15)gi1 = (5)h12] - (5)h5 = (5-7)b5 = b6 - fi6 = (7)FXWfi47i9 => g7≠7; UP 44: NP(38)c67 => c2349≠38; UP 81

Digressive Preaching: A slightly nasty AAIC in that last step. Rather than looking directly for such an animal, one could solve the puzzle using shorter steps and then take that knowledge to construct a fewer step solution. Simply put, that is exactly how I arrived at the step minimizing path above. I find it more instructive to know how to find such an animal by recognizing the little pieces of logic, or steps, that collaborate to create the beast.