Again for March 21, 2007 - Y Wing Style

The following is an illustrated proof for the Tough Sudoku of March 21, 2007. The primary advanced keys used in this proof are coloring and Y wing styles.

You may need to refer to previous blog pages to understand this proof. Links to these pages are found to the right, under Sudoku Techniques.

Often during this illustration, there are many other steps available. It is not the goal of this page to show every possible step, but rather to illustrate steps that, taken together, unlock this puzzle in a relatively simple fashion.

To understand this page, some previous blog pages that could be particularly helpful are:

• Locked Candidates
• Pairs, Triples, Quads.
• Forbidding Chains 101 The Theory
• Y Wing Styles
• Finding Y Wing Styles
• Coloring
• Finding Coloring
• Definitions: If a term is used on this page that you do not understand, the definition is likely here!

The illustrations of forbidding chains used in this proof will share the same key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define the partitioning of native strong inference sets
• candidates crossed out in red = candidates proven false

Strong and weak need not be mutually exclusive properties.

Puzzle at start

Hidden Pair 79

From this point,(borrowing a trite phrase), there exists an almost endless variety of manners to proceed. The following is the most efficient path that I found.

Locked candidate 2

Coloring with 9s (2 string kite)

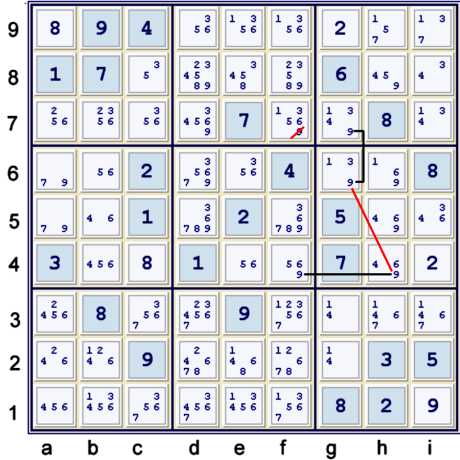
Illustrated above is a two strong set chain using candidate 9:

• g7 == g6 -- h4 == f4 => f7≠9

To convince oneself of the validity of the elimination, one can use the following proof by contradition:

• Let f7=9
• => f4,g7≠9 => g6=h4=9 => impossible, too many 9s in box h5

Y Wing Style using 349

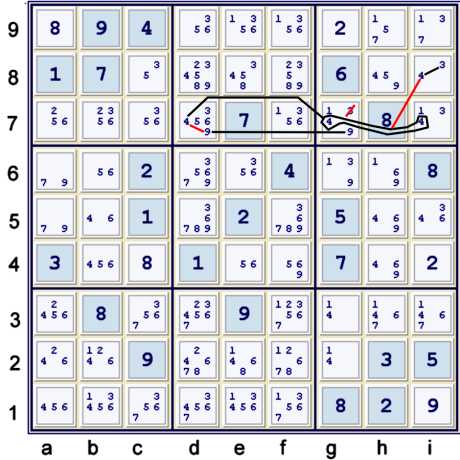
The chain illustrated above becomes more obvious if one uses pair 14 at g23 first. Nevertheless, the elimination is available as shown above without making that step. As a forbidding chain or Alternating Inference Chain (AIC):

• i8=3 == i8=4 -- gi7=4 == d7=4 -- d7=9 == g7=9 => g7≠3

This Y Wing Style elimination uses the 4s in row 7 as the vertex, considering them in two groups

1. d7=4
2. gi7=4

As such, the logic that conforms to typical Y Wing Style logic follows:

• d7=4 => d7≠9 => g7=9 => g7≠3
• gi7=4 => i8≠4 => i8=3 => g7≠3

After making this elimination, a few cells are solved by Unique Possibilities:

• g6 = 3% column
• g7 = 9% column
• h6 = 1% row & box

Naked Pair 56

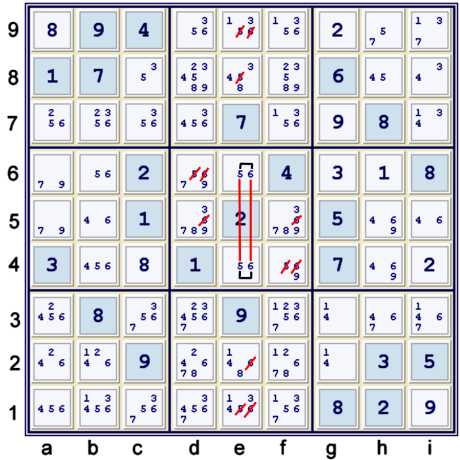
The pair 56 above is illustrated as a wrap-around forbidding chain:

• e6=6 == e6=5 -- e4=5 == e4=6 =>
• 56 is forbidden from the rest of column e and box e5

This begins a cascade of Unique Possibilities beginning with f4 = 9% cell. This cascade advances the puzzle to 46 cells solved (UP 46).

Locked Candidate 6

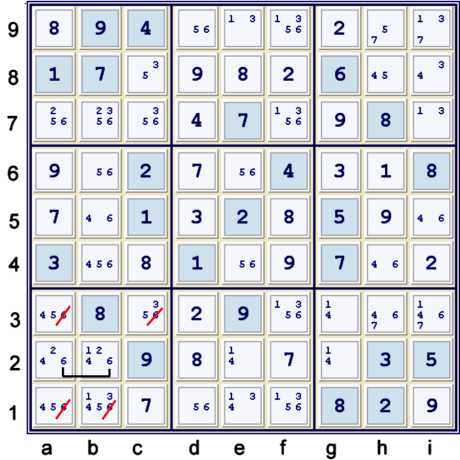
Illustrated above, the sixes in row 2 are limited to only ab2, thus eliminating sixes from the rest of box b2. This begins another cascade of Unique Possibilities (a few hidden singles, then naked singles) that brings the puzzle to completion. (UP 81).

If one had performed many of the other possibile eliminations earlier, one may have used a standard Y wing instead of the Y Wing Style illustrated. Also, one may have proceeded to the end a bit differently (For example, if one uses locked 6s at b456 earlier, then the puzzle unlocks after any number of possible Y Wing Styles. Most of these will require the coloring step with the 9s.)

Solution

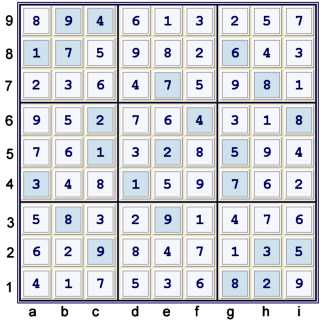
Proof

One of many possible proofs for this one:

1. Start at 23 filled - the given puzzle. Unique Possibilities to 25 filled. (UP 25).
2. Hidden pair 79 at a56 forbids a6=56, a5=468, a123=7 UP 27
3. Locked 2s at ab7 forbids dfg7=2 UP 28
4. 1. fc on 9s: g7 == g6 -- h4 == f4 forbids f7=9
   2. Y Wing Style: i8=34, gi7,d7=4, dg7=9 forbids g7=3 UP 31
5. Pair 56 at e46 forbids e189d6f4=5 and forbids e129,d56,f45=6 UP 46
6. Locked 6s at ab2 forbids ab1ac3=6 UP 81

• Sets: 2 + 1 + 2 + 3 + 2 + 1 = 12
• Max depth 3 at step 4.2
• Rating: 2(.01) + 3(.03) +.07 = .18

Notes

Since this puzzle can be solved using the Simple Sudoku solving set, one might consider it to be too easy for a tough puzzle here at sudoku.com.au. However, the path that I have illustrated here involves much fewer steps, and much less native puzzle information, at less maximum depth, than the solution provided using Simple Sudoku Hints. This puzzle is therefor not a very difficult puzzle.

This puzzle is a good exercise, though, in using multiple techniques. It also is an excellent exercise in the theme of the last few days: Y Wing Styles.

BTW, I have no control over the puzzles that are selected here. It has just been a happy accident that I have been able to showcase Y Wing Styles this many days in a row.

Y wing Style eliminations are available in most tough sudoku puzzles, across all sites that I have visited.