The following is an illustrated proof for the
Tough Sudoku of March 25, 2007.
This is a very easy puzzle, and only requires one to know one technique,
Coloring. One may wish to also refer to the
page on Finding Coloring.
You should not need to refer to previous blog pages to understand
this proof. However, links to these pages are found to the right, under Sudoku Techniques.
Puzzle at start
Some Unique Possibilities are available here.
- f4 = 5% box
- f4 is the only 5 possible in the box
- e5 = 3% box and row
- e5 is the only 3 possible in both the box and the row
I call these two cell solutions Unique Possiblities (UP).
Possibility matrix at UP 24
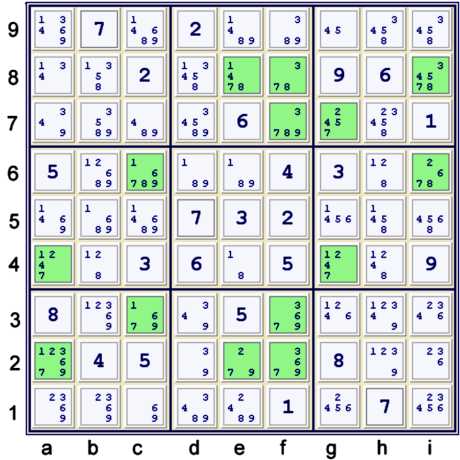
Above is the current possibility matrix. At this point, although there are some other steps
possible, I noticed that the 7s are interesting. Above, all the remaining possible locations for
7 are highlit.
I found many ways to significantly advance the puzzle considering only the 7s. One can pick
any one of the following three and one will eventually arrive at the same puzzle.
Coloring on 7s Example 1
Consider a24=7 as a vertex:
- a4=7 => g4≠7 => g7=7 => f7,i8≠7
- a2=7 => e2≠7 => e8=7 => f7,i8≠7
As a
forbidding chain or
Alternating Inference Chain (AIC) on 7s:
- e8 == e2 -- a2 == a4 -- g4 == g7 => f7,i8≠7
Coloring on 7s Example 2
Consider fg7=7 as a vertex:
- f7=7 => f3≠7 => c3=7 => a2,c6≠7
- g7=7 => g4≠7 => a4=7 => a2,c6≠7
As a
forbidding chain or
Alternating Inference Chain (AIC) on 7s:
- c3 == f3 -- f7 == g7 -- g4 == a4 => a2,c6≠7
Coloring on 7s Example 3
Consider i68=7 as a vertex:
- i6=7 => c6≠7 => c3=7 => a2,f3≠7
- i8=7 => e8≠7 => e2=7 => a2,f3≠7
As a
forbidding chain or
Alternating Inference Chain (AIC) on 7s:
- c3 == c6 -- i6 == i8 -- e8 == e2 => a2,f3≠7
After making any of the eliminations listed above, all but 2 of the 7s are solved, plus
a few more Unique Possibilities. This brings the puzzle to 36 cells solved (UP 36).
Possibility matrix at UP 36
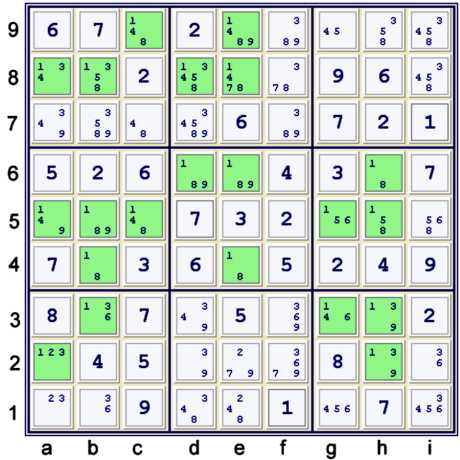
Above is the current possibility matrix. At this point, again there are some other steps
possible, but here I noticed that the 1s are interesting. Above, all the remaining possible locations for
1 are highlit.
I found many ways to advance the puzzle considering only the 1s. Below, find
four of them. The last one in the group is the most powerful, as it unlocks the puzzle into only
Unique Possibilities.
Coloring on 1s Example 1
One way to see the logic above follows:
- c9=1 => e9≠1
- c9≠1 => c5=1 => b4≠1 => e4=1 => e9≠1
As a forbidding chain on 1s:
- c9 == c5 -- b4 == e4 => e9≠1
Coloring on 1s Example 2
One way to see the logic above follows:
- d8=1 => b8≠1
- d8≠1 => d6=1 => e4≠1 => b4=1 => b8≠1
As a forbidding chain on 1s:
- d8 == d6 -- e4 == b4 => b8≠1
Coloring on 1s Example 3
One way to see the logic above follows:
- c9=1 => b8,c5≠1
- c9≠1 => e9=1 => e4≠1 => b4=1 => b8,c5≠1
As a forbidding chain on 1s:
- c9 == e9 -- e4 == b4 => b8,c5≠1
Coloring on 1s Example 4
One way to see the logic above follows:
- g3=1 => b3≠1
- g3≠1 => g5=1 => abc5≠1 => b4=1 => b3≠1
As a forbidding chain on 1s:
- g3 == g5 -- abc5 == b4 => b3≠1
Notes
Looking at the puzzle, this last example seems most powerful. Why? After making the
elimination, clearly a2=1, then one can find hidden singles that solve all the 2s, then all the
7s, then all the 6s, then another 1, and then a 4. Now the puzzle is reduced to naked singles to
the end.
The use of a grouped argument in coloring, and in fact in all of sudoku techniques, is a
common trick that is very useful. Such grouped arguments have many fancy names, but regardless
of what one calls them, they are simply a grouping of possibilities. Since such groupings are
very helpful, including them in one's bag of tricks is strongly advised.
One may note in the proof below, I choose to group the 1s a different way to achieve the same
result. Sometimes, realizing these different possible groupings could also be helpful.
Proof
- Start at 22 filled - the given puzzle. Unique Possibilities to 24 filled. (UP 24).
- fc on 7s: e8 == e2 -- a2== a4 -- g4 == g7 forbids f7=7 UP 36
- fc on 1s: b45 == ac5 -- g5 == g3 forbids b3=1 UP 81
- Sets: 5
- Max depth 3
- Rating: .10
Again, a puzzle that is probably too easy for the tough label!