The following is the second page of an illustrated solution for the
sudoku.com.au tough puzzle of 12/21/07. The
previous page primarily attacked candidates
78 and their grid interactions. This page will continue that theme, but add a few wrinkles.
If this is your first visit to this blog, WELCOME!!
Previous blog pages may be helpful. Links to these pages are found to the right,
under Sudoku Techniques.
The illustrations of steps shown on this page will share this key:
- black line = strong inference performed upon a set (strong link)
- red line = weak inference performed upon a set (weak link)
- black containers define a partioning of a strong set(s)
- candidates crossed out in red = candidates proven false
Please be aware that, for me,
strong and weak need not be mutually exclusive properties.
There are many possible deductions and eliminations not taken on this page. The one's that are shown below
have been picked either for their utility for this particular puzzle, or for their instructive power, or simply because
they seemed elegant to me.
Step 2j An easy Uniqueness elimination
This deduction has been available for quite some time.
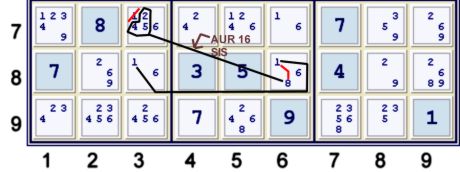
If cells r78c3 and r78c6 are limited to only candidates 16, then those cells cannot be resolved. In fact, those
cells would be isolated from the puzzle. This isolated portion would have two solutions. Thus, the puzzle could not
have exactly one solution. Hence, this situation is known impossible. Since cells r8c3 and r7c6 are already limited to
only candidates 16, it is trivial to build the AUR sis: (245)r7c3=(8)r8c6. The following short chain is then available:
- (245)r7c3=(8-1)r8c6=(1)r8c3 => r7c3≠1
Digression
It has been asserted (elsewhere) that if one is to utilyze AUR, then one should make
all such AUR deductions at once, since one loses the AUR power after destroying
the AUR possibility. This assertion is false. If any Uniqueness sis be true, they
are ALWAYS TRUE for that puzzle. Any assertion otherwise is not logical.
In my opinion, the true power of uniqueness considerations in Sudoku have not yet been fully utilyzed.
It may be, with uniqueness considerations, just as good to maintain the weak inference sets.
For example, above the two cells limited to (16) imply (1-1) and (6-6) at the corners, yielding the following
shorter AIC:
- (1)r8c6=(1)r8c3 => r7c3≠1
Step 2k
Again, this deduction has been available for quite some time.
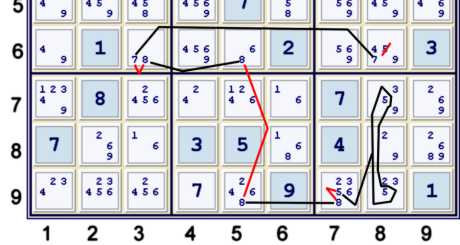
This rather mundane elimination is really just part of the set up for the next few steps. One can write:
- (5)r79c8=(5-8)r9c7=(8)r9c5-(8)r6c5=(8-7)r6c3=(7)r6c8 => r6c8≠5
Step 2l
This deduction is newly available in this shortened form because of the previous step.
Above, one could have used the almost hidden pair 49 in box 5 to reach the same conclusion. In fact there are
many ways to get this elimination. The way I choose to illustrate could be written:
- (6=8)r6c5-(8=pair35)r45c6-(5)r6c4=(5)r6c7 => r6c7≠6
- => step 2m Locked 6s r45c6 => r5c4≠6 (not illustrated)
Step 2n
Above, the almost naked pair 16 r8c36 is an important key.
- (pair16=8)r8c36-(8)r9c5=(8-6)r6c5=(6)r6c4-(6)r2c4=(6)r2c2 => r8c2≠6
- => step 2o (Pair29)r8c28 => r8c9≠29 (not illustrated)
Step 2p A nettish step using cell r2c8
The newly stronger 2s in row 8 make the next step much easier to find.
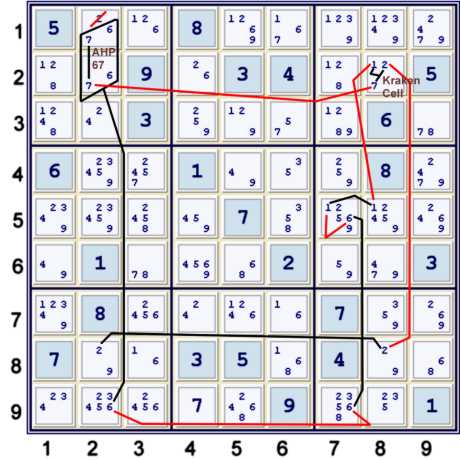
Above, the choice to eliminate 2 from r1c2 is arbitrary, as one could just as easily eliminate 6 from r9c2. The
Kraken cell consideration of all possible values for cell r2c8 is key. Note that the stronger 6s in column 7 from step
2l are also important.
- (Hidden Pair 67)r12c2=(6)r9c2-(6)r9c7=(6-1)r5c7=(1)r5c8-(1)r2c8=*
- [(7)r1c2=(7)r2c2-(7=*2)r2c8-(2)r8c8=(2)r8c2]
- => (67)r1c2=(2)r8c2 => r1c2≠2
- => step 2q (pair67)r12c2 => r1c3,r9c2≠6 (not illustrated)
Another way to write step 2p (there are always many ways for such nets):
- (7)r1c2=(7)r2c2-(7)r2c8=*
- [(2)r8c2=(2)r8c8-(2=*1)r2c8-(1)r5c8=(1-6)r5c7=(6)r9c7-(6)r9c2=(HP67)r12c2]
- => sis[(hp67)r12c2,(7)r1c2,(2)r8c2] => r1c2≠2
Probably, I prefer the latter presentation.
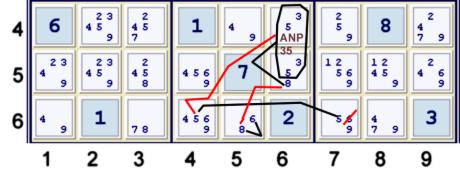
Step 2r Prelude
Below, I build a strong inference set (sis) based upon the AUR16 r17c56 (Almost Unique Rectangle). There are many ways to do this, and
there are many short deductions possible from the resultant possible sis's. However, I choose to build the following
one as it eventually catches quite a few of the possible eliminations. Maybe it catches them all.
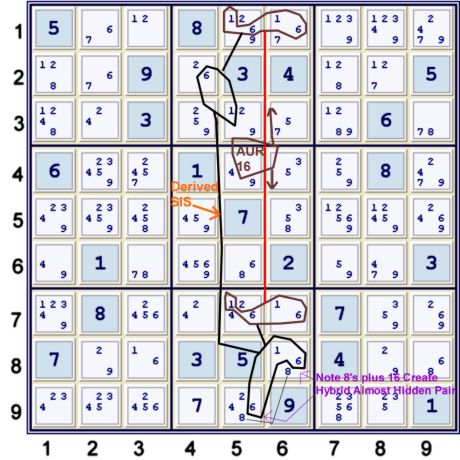
Above, one could write:
- [(1)r3c5=(6)r2c4]=(hp16)r1c56-AUR(hp16)r7c56=[(16)r8c6=(6)r9c5]
- =>AUR sis [(1)r3c5,(6)r2c4,(16)r8c6,(6)r9c5]
- now, consider (8)r8c6=(8)r9c5. Combine this super cell with the AUR sis
- => sis[(1)r3c5,(6)r2c4,(Hybrid Hidden Pair 168)r8c6,r9c5]
This
hybrid hidden pair is a newly coined term, I think. Really it is just a natural extension of the
Super Cell concept. It serves as a way to efficiently and logically reduce the size and complexity of this
particular AUR sis. The potentially five-headed sis is thus reduced to a three-headed sis. One still likely needs
a net to handle any deductions from this sis, however the potential net complexity is significantly reduced.
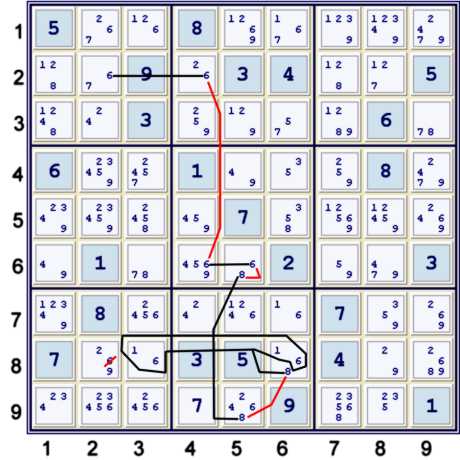
Step 2r An AUR net using Kraken Column 1s
The potential interaction of candidate 1 with candidate 8 in boxes 8 and 1 are key to this elimination group.
I found this group using the counting method of net analysis. The count went as follows:
- (8)box 8 (+2) - note I have not yet decided 8's are an endpoint!
- (8)box 5 (+0) - regardless of what I do, these (8)'s are added free of charge. I may decide later
to use a different strong 8 link - as illustrated below
- (6)box 5 (+0)
- (8)c9 (+0)
- (8)r2 (+0) the candidate 8 grid strength is fairly prevasive, and worth considering in total
- (1)r8 (+0)
- (1)c1 (+0) because of the 8 interactions, the Kraken column 1s are added at no charge
- AUR sis (+0) - since I can now add the AUR sis at no charge, it is time to figure out what I may have
- Place (68)r9c5 both in result column (-2) total zero. Done.
One can now easily build the implied
Triangular Matrix. One can also rewrite the deduction into a bit
of scrambled AIC form. Note that the hybrid almost hidden pair concept is key, but not actually required in the counting
method. Nevertheless, I find it useful as it tells me that counting will be reduced.
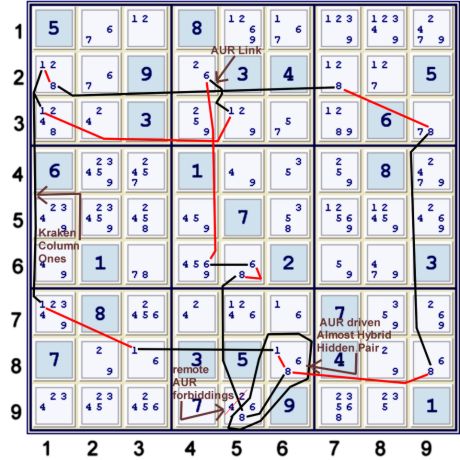
The deduction above can be written as AIC in many ways. Here is one:
- (hybrid hidden pair68)r8c6,r9c5=*AUR
- [(8)r9c5=(8-6)r6c5=(6)r6c4-(6)r2c4=*AUR(1)r3c5-(1)r3c1=**
- [(1)r8c6=(1)r8c3-(1)r7c1=**(1-8)r2c1=(8)r2c7-(8)r9c3=(8)r8c9]-(8)r8c6=(8)r9c5]
- => (hybrid hidden pair 168)r8c6,r9c5=(8)r9c5
- => (6=8)r9c5 => r9c5≠24
This is by far the most difficult elimination used in this solution. However, it serves to significantly unlock the puzzle.
Since it is very powerful, I judged it to be worth the effort.
Steps 2s, 2t, 2u combined
A few easy eliminations follow
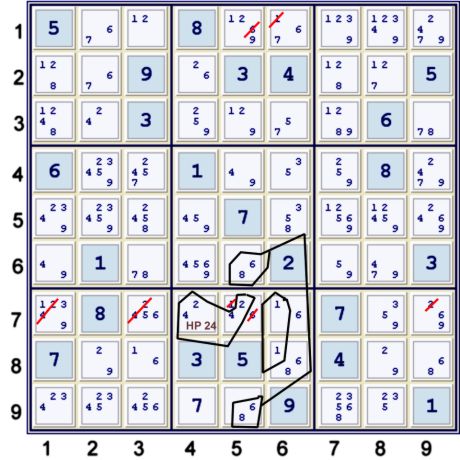
The three steps: (note step 2u requires step 2s precede it)
- 2s) (Hidden pair 24)r7c45 => r7c5≠16, r7c139≠24
- 2t) (Naked pair 68)r69c5 => r1c5≠6
- 2u) Locked 1s r78c6 => r1c6≠1
This sets the stage for a very pretty step - at least I find it pretty!
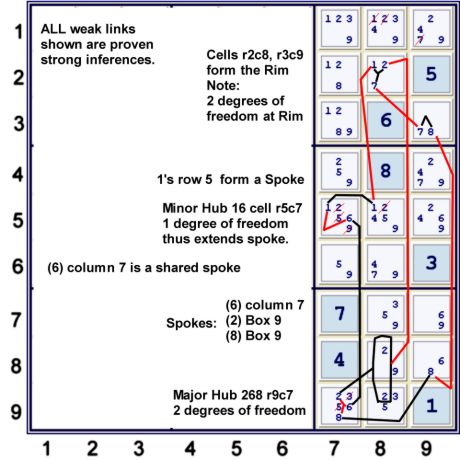
Step 2v A wrap around net - Also known as a Hub, Rim & Spokes.
The previously considered Kraken Cell r2c8 now forms part of the Rim for a nice elimination group. Note
that each individual forbidding occurs in only one dimension. This means that this net can be expressed as a
Symmetric Pigeonhole Matrix. Therefor, every weak link set considered is proven to be a strong inference set. Again,
a simple counting exercise can reveal this group: (One can start anywhere, so the choice order below is completely
arbitrary)
- (127)r2c8 (+2) - this means that at least one of 127 will be in the result column
- (1)r5c87 (+0)
- (6)c7r59 (+0)
- (2)r89c8,r9c7 (-1), total (+1) - note that (2)s is linked to both the column 7 6s and (127)r2c8
- (78)r3c9 (+0)
- (8)r8c9,r9c7 (-1), total (0) - done.
- recognize that this is a symmetric pm. The only multi-weak link node is r9c7, and all the weak links there
are intercellular links (the same dimension). Thus we can safely eliminated any item seen by both ends of each weak link
I have attempted to label the parts of this animal above. The usefulness of this categorization is questionable.
If the labels serve to add confusion, kindly ignore them. The deduction stands on its own without needing a name for
its parts. However, since it has been named, I thought it wise to recognize that fact. Because this deduction is
analygous to naked sextuplet, it does not easily transfer into AIC. Rather than attempt that exercise, below find the symmetric
pigeonhole matrix.
| r2c8 |
1 |
2 |
7 |
|
|
|
| r3c9 |
| | 7 | 8 |
| |
| 8B9 |
| | | r7c9 |
r9c7 | |
| 2B9 |
| c8 | | |
r9c7 | |
| 1r5 |
c8 | | | |
| c7 |
| 6c7 |
| | | |
r9 | r5 |
Since each column is a proven sis,
- (1):r5c8=r2c8 => r1c8≠1
- (2):r89c8=r2c8 => r15c8≠2
- (7):r8c2=r9c3 => r9c1≠7
- (8):r3c9=r8c9 => nothing, we already had that
- (2=6=8)r9c7 => r9c7≠35
- (1=6)r5c7 => r5c7≠259
- After making these eliminations, (3)r1c7 %column => UP 25, finally!
At this point, the puzzle is significantly undone. A few relatively easy
steps remain. The puzzle will be finished off on the
next page.