Easter Sudoku Proof

The following is an illustrated proof for the Tough Sudoku of April 8, 2007. The main techniques that I used to solve this puzzle are forbidding chains, which are called at most sudoku sites Alternating Inference Chains (AIC).

Happy Easter to everyone! I would feel guilty publishing a blog page on Easter Sunday, but it is only Saturday at my location on this orb.

You may wish to refer to previous blog pages to properly understand this proof. Links to these pages are found to the right, under Sudoku Techniques.

This page illustrates only the deduced elimination steps that I choose to solve the puzzle. Although many other steps are possible, they are not shown, as to show every possible step is prohibitive in both time and space!

The information on the following blog pages may be helpful:

• Locked Candidates
• Pairs, Triples, Quads
• Almost Locked Sets
• Forbidding Chains 101 The Theory
• Definitions: If a term is used on this page that you do not understand, the definition is likely here!

The illustrations of forbidding chains used in this proof will share the same key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a grouping of strong inference set(s)
• candidates crossed out in red = candidates proven false

Strong and weak need not be mutually exclusive properties.

Puzzle at start

Although I only show a few steps here, the search for more complex techniques usually begins for me only after exhausting the easy stuff. After solving the puzzle, to make the proof as short as possible, I can easily see which of the steps that I found were not required.

Locked candidate 8

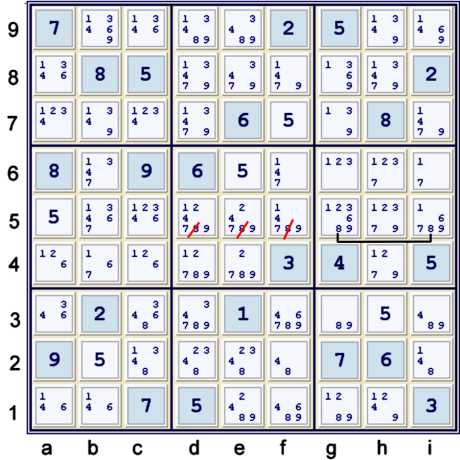
Above, the 8s in box h5 are limited to only gi5. Since gi5 exists in row 5, the possible 8s in row 5 and outside of box h5 cannot exist. You may note that there is a hidden pair 68 at gi5. I did not need the hidden pair in this proof, but there are other proofs possible that would likely use this hidden pair. The beginning of such an alternate path will be placed at the end of this proof.

There are quite a few very pretty wrap around, or continuous nice loop chains available here. Since my time was short, I choose not to detail those and instead picked the chain above for this proof. Probably, a better proof is possible considering some of the chains more strongly indicated by my standard puzzle marks

Almost Hidden Pair used in a chain

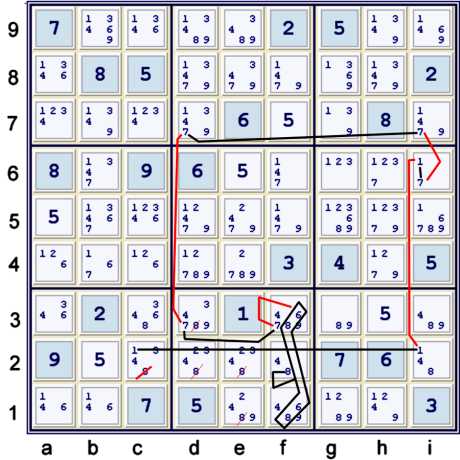
Above, I use the Almost Hidden Pair 68 at f13 in a chain. The chain could be written as:

• f2=8₁ == {Hidden Pair 68₁ at f13} -- f3=7 == d3=7 -- d7=7 == i7=7 -- i6=7 == i6=1 -- i2=1 == c2=1
• => c2≠8
• Also, since the chain uses the Locked 8s at f123, => e12,d23≠8

The latter eliminations are just a reflection of being efficient, and generally I would have made those eliminations first.

The logic behind this step is as follows:

• f2=8 or f13 is restrained to only candidates 6,8 as there would be only 2 locations left for both 6,8 in column f.
• The rest of the chain is standard fare

To convince yourself of the validity of the elimination, see what happens to the sets indicated on the illustration if c2=8. Feel free to ask me if you cannot follow the logic, as I may detail it better when I have more time.

After making the eliminations noted above, 3 cells can be solved:

• c3 = 8% column and box (hidden single)
• g3 = 9% cell
• i3 = 4% cell

Standard depth 5 chain using candidates 679

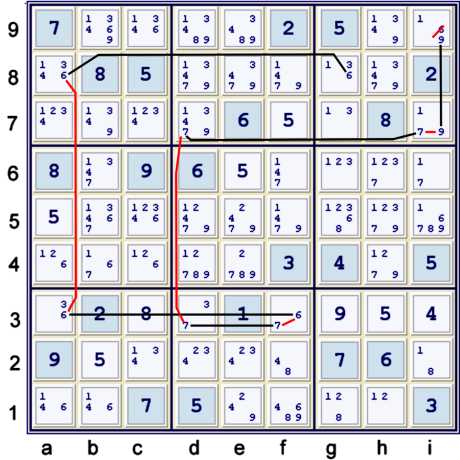
Illustrated above is a standard forbidding chain:

• i9=9 == i7=9 -- i7=7 == d7=7 -- d3=7 == f3=7 - f3=6 == a3=6 -- a8=6 == g8=6
• => i9≠6

This chain is not hard to find, as it considers some of the same strong inferences used in the previous chain. It is probably not the shortest chain possible to unlock this puzzle, but it does the trick nonetheless. After eliminating the 6 from i9, the puzzle is reduced to a cascade of Hidden and Naked singles (Unique Possibilities) to the end.

Proof

1. Start at 22 filled - the given puzzle. Unique Possibilities to 27 filled. (UP 27)
2. 1. Locked 8s at gi5 forbids def5=8
   2. f2=8 == hp 68 at f13 -- f3=7 == d3=7 -- d7=7 == i7=7 -- i6=7 == i6=1 -- i2=1 == c2=1
      • forbids c2=8 and forbids d23,e12=8
3. i9=9 == i7=9 -- i7=7 == d7=7 -- d3=7 == f3=7 -- f3=6 == a3=6 -- a8=6 == g8=6
   • forbids i9=6 UP 81

• sets: 1 + 6 + 5 = 12
• Max depth 6 at step 2.2
• Rating: .01 + .63 + .31 = .95, high rating due to one long step!

Notes

An alternative path partially detailed below. After making all the standard easy eliminations, the following chains are possible as a starting point for probably a more efficient, meaning lowered rating, proof:

• a8=6 == g8=6 -- g5=6 == g5=8 -- g1=8 == f1=8 -- f1=6 == f3=6
  • forbids a3=6
• c3=8 == c2=8 -- c2=1 == i2=1 -- i6=1 == i6=7 -- i7=7 == d7=7 -- d3=7 == f3=7 -- f3=6 == c3=6
  • forbids: c3=34, c2=34, i79=1, d458=7, f3=489 (wrap around chain) UP 28

Now, perhaps a depth 3 or depth 4 chain(s) and some locked candidates, maybe a pair depending on path, can unlock the puzzle. I would love to see alternative proofs for this one, as I am certain that better ones are possible than the one illustrated above.