Extreme Diabolic Tough April 12, 2007 Final Page

Still with me?! Congratualations on struggling through this far. The following blog pages are still prerequisites for understanding this page:

• Advanced Forbidding Chains The theory of using techniques within Chains
• Definitions

This page is still challenging. I am still open for questions.

If you missed the first page of this puzzle proof, it can be found here.

If you missed the second page of this puzzle proof, it can be found here.

An Almost Y wing used in a chain

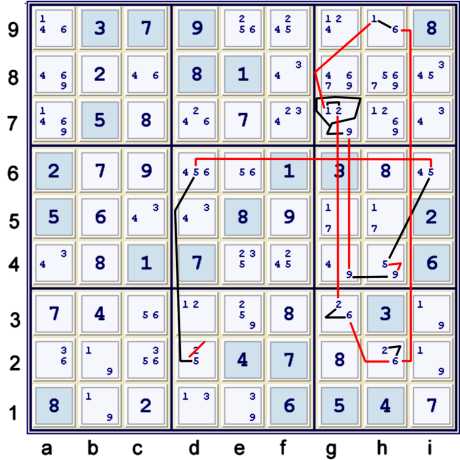
If one gets fairly proficient at all Y wing Styles, they become natural components of forbidding chains. They can take the form of Almost Y Wing Styles. Above, the illustration shows:

• d2=5 == d6=5 -- i6=5 == h4=5 -- h4=9 == g4=9 -- g7=9 == {Y wing f3=62, f7=21, h9=16} -- h2=6 == h2=2
  • => d2≠2

Again, it is essential that the bracketed Boolean, in this case a standard Y wing, or xy wing, fully forbid the weakly linked condition - in this case h2=6. Also, that the Boolean exists when the strongly linked condition is false, in this case, g7=9. Again, the logic is basically the same as all the other complex forbidding chains used in this proof.

Finding this one is almost a self-fullfilling prophecy. The easiest eliminations that I could find cleared away much debris from cells g7,h9. Thus, it was natural to look for a way to use the remaining possibilities there in a chain.

After forbidding 2 from d2, a few cells finally solve

• d2 = 5% cell
• c3 = 5% box & row & column
• g3 = 6% row
• h2 = 2% box, row, column & cell

The worst is over. But there remains another very interesting step.

Almost Coloring, Almost Locked Set, all within a forbidding chain - again!

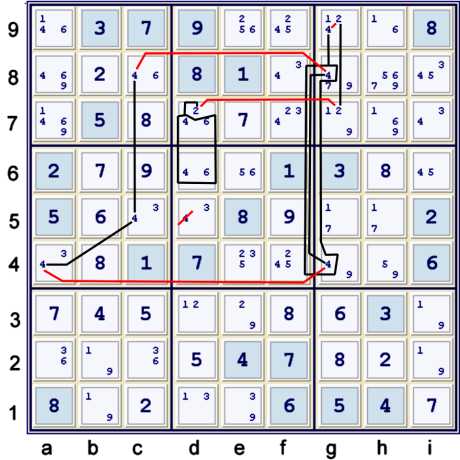
This one is a bit atypical. One could write it a different way, but I have chosen this presentation:

• {pair 46 at d67} == d7=2 -- g7=2 == g9=2 -- g9=4₁ == {fc on 4s: c5 == a4 -- g4 ==₁ g8 -- c8 == c5}
  • => d5≠4

All the possible 4's in column g are considered in this chain. What makes this presentation interesting is that the bracketed Boolean fc on 4s.... starts and ends with the same argument: c5. This means that if that Boolean be true, than c5=4. Thus, the chain reduces to merely:

• {pair 46 at d67} == c5=4

Note that c5=4 lies at the intersection of four strong links, (one bivalue, three bilocation). This makes c5 a very likely focal point for some sort of chain.

The trick of letting the fc on 4s prove a cell is true is also nothing new. Many times, one can do this even with standard chains. In this case, one could have written the fc on 4s to either forbid a4=4 or c8=4. But, in either case, the strong links; a4 == c5, c5 == c8, would eventually need considering. Thus, the manner in which I choose to write the chain seemed most efficient. Nevertheless, what I saw was more like a conditional sky scraper plus an ALS, with some linkage between them.

After d5≠4, quite a few cells solve. The entire bottom third of the puzzle grid is reduced to naked singles. Nevertheless, this puzzle is resistant still.

Almost Locked Set in a Chain

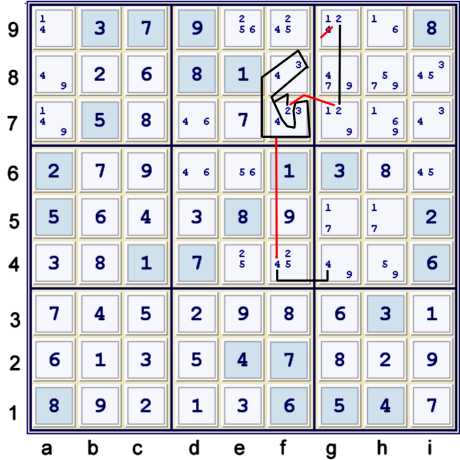
Above, the following relatively easy chain:

• g9=2 == g7=2 -- f7=2 == {pair 34 at f78} -- f4=4 == g4=4 => g9≠4

Any time during this process, one could have used the Almost Unique Rectangle formed by f8=34, i7=34 and the strong 3s at fi78. I have chosen not to do so because I prefer to prove the solution is unique, and because it did not seem to advance the puzzle significantly. For example, if one had used the AUR, then e8≠4 => e8=i7=3. The chain above would become a standard Y wing style using only three native strong inference sets. I found such nominal help failed to justify the price of using the AUR.

Neverthless, if one is solving for speed, the AUR may be a good choice. (Much earlier!)

Naked Quad 1269

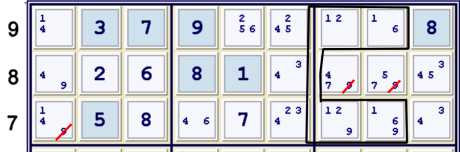
It is rare that this late in a puzzle, one would need forbidding chains. It is even more rare that one could still use a naked quad. Finally, it is rarest of all that the naked quad can only be replaced with a hidden quad. This late in the puzzle, one would expect perhaps a hidden pair versus a naked quad. But, I suppose, this one is meant to be difficult, even when doing the easy stuff! After making the eliminations justified by the Quad shown above, a8 = 9% row, column & box.

Final Chain

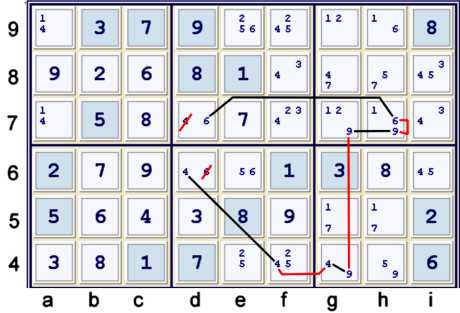
The chain illustrated above at least has some sort of pretty symmetry to it. I suppose that makes it a fitting final chain for this puzzle. With the puzzle almost reduced to just 4 boxes, there are possible chains everywhere. I did not spend any time looking for efficient ways to finish this one off. I just wanted to get it done! The chain above should be self explanatory, if you have made it this far!

The Solution

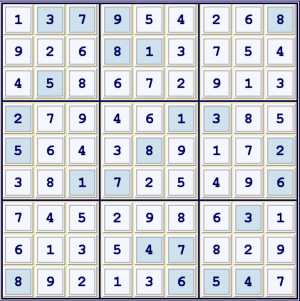
PROOF

1. Start with the given puzzle. Unique Possibilities to 28 filled. (UP 28)
2. 1. Hidden pair 78 at bh6 forbids b6=469, h6=59
   2. Locked 9s at e13 forbids e46=9
   3. Pair 19 at i23 forbids g23h2i678=9 and forbids g23h2i7=1 UP 29
3. fc on 3s: a2 == a4 -- e4 == e1 forbids c1,d2=3 UP 31
4. b8=4 == a789=4 -- a4=4 == a4=3 -- a2=3 == c2=3 -- c2=5 == c3=5 forbids c3=4 UP 37
5. Pair 34 at cd5 forbids fg5=4, f5=3 UP 38
6. 1. Pair 19 at bi2 forbids ad2=1, a2=9
   2. Very common Y style: d5=34, di6=4, i7=34 forbids d7=3
   3. Locked 3s at f78 forbids f4=3
   4. d3=1 == d1=1 -- d1=3 == d5=3 -- c5=3 == c2=3 -- c2=5 == d2=5 forbids d3=5
   5. d7=6 == d6=6 -- d6=5 == d2=5 -- c2=5 == c3=5 -- c3=6 == g3=6 forbids g7=6
   6. {fc on 4s:d7 ==* d6 -- i6 == i78} == d5*=4 -- d5=3 == e4=3 -- e4=2 == f4=2 -- f7=2 ==pair 34 at di7 forbids g7=4
   7. g9=4* == {fc on 4s: g8 ==* g4 -- a4 == c5} -- c8=4 == c8=6 -- c3=6 == g3=6 forbids g9=6
   8. e9=2 == pair 56 at e69 -- e3=5 == f2=5 -- f2=2 == h2=2 forbids h9=2
   9. h9=6 ==*{ d6=6 == d7=6 -- e9=6 ==* a9=6 -- c8=6 == c8=4 -- c5=4 == d5=4} -- d6=4 == i6=4 -- i6=5 == i8=5 forbids h9=5
   10. Locked 5s at hi8 forbids f8=5
   11. d2=5 == d6=5 -- i6=5 == h4=5 -- h4=9 == g4=9 -- g7=9 =={xy wing 62,21,16 at g3,g7,h9} -- h2=6 == h2=2 forbids d2=2 UP 42
7. {fc on 4s: c5 == a4 -- g4 ==*g8 -- c8 == c5} ==*g9=4 -- g9=2 == g7=2 -- d7=2 == pair 46 at d67 forbids d5=4 UP 56
8. 1. g9=2 == g7=2 -- f7=2 == pair 34 at f78 -- f4=4 == g4=4 forbids g9=4
   2. Naked quad 1269 at gh79 forbids gh8=9 UP 57
9. d7=6 == h7=6 -- h7=9 == g7=9 -- g4=9 == g4=4 -- f4=4 == d6=4 forbids d7=4,d6=6

• sets:2+1+2+2+4+2+2+3+1+4+4+6+4+4+6+1+7+6+4+4+4 =
  • 3(1)+ 5(2) + 1(3) + 8(4) + 3(6) + 7 = 73 (VERY HIGH!)
• Max depth 7 at step 6.11 (High, but not terribly so)
• Rating: 3(.01) + 5(.03) + .07 + 8(.15) + 3(.63) + 1.27 = 4.61
  • Almost worthy of the label: unsolvable.

NOTES

I shall not fully illustrate proofs of such puzzles very often, as it consumes both more time and more effort than I intend to expend. However, I really wanted to demonstrate using Almost Forbidding Chains, or Almost Alternating Inference Chains. This puzzle seemed like a good one to use. Kindly place any comments or questions about this proof on the page where the question arises. I receive automatic notification of you comments, so I shall find them. Eventually, I will even answer them!