Solution for Tough of November 28, 2007 Page Two

The following is page two of an illustrated solution for the Tough Sudoku of November 28, 2007. This page has two steps which are interesting. One of these two steps employs both

• The recognition of a useful Almost Y Wing Style
• Counting to extend the chain/net

Page One of this solution was primarily about the use of an Almost Unique Rectangle in a chain. The Sudoku tips and tricks contained on this page are less atypical.

Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. This list is getting long, so specifically, one may want to refer to the following previous blog pages:

• Locked Candidates
• Pairs, Triples, Quads
• Y Wing Styles
• Finding Y Wing Styles
• Forbidding Chains 101 The Theory
• Almost Locked Sets
• ALS Proof of 03/10/07
• A study in chain forging page 4. Super cells were introduced there, and they continue to make some of the steps below easier to find.
• Matrices in Sudoku. The theoretical foundation for counting is poured.

The illustrations of steps shown in this solution path will share the following key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set(s)
• candidates crossed out in red = candidates proven false

Please be aware that, for me, strong and weak need not be mutually exclusive properties.

Step 3a - a wrap around, or continuous, Y Wing Style

Typically, this type of Y Wing Style will employ at least one grouped argument, such as (3)r5c5=(3)r5c23 above.

After making the indicated eliminations, the next step is easy and not illustrated:

• 3b Locked candidate 7 r4c56 => r6c56≠7

Step 3c - Y Wing Style plus one sis

It is always nice when two chains overlap in this fashion allowing both eliminations at once. Of course, one could have alternatively written:

• (Hidden Pair 57)r4c56=(5)r6c6-(5)r6c13=(5-1)r5c3=(1)r4c1 => r4c56≠1

The latter presentation is quite compliant with the concept of Super Cells. Thinking in this manner makes the chain-finding easier. Also, it makes it less likely that one would miss an elimination.

Step 3d - Almost Locked Sets chained together a bit

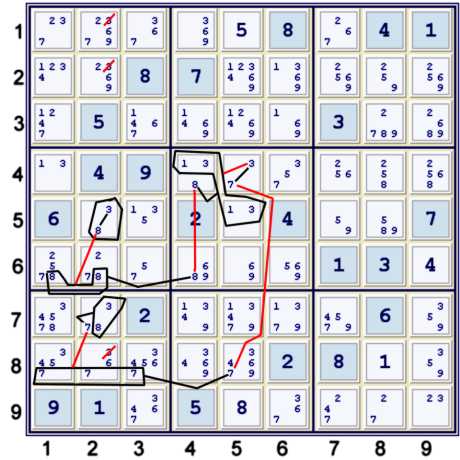
Above, a slightly long but relatively easy chain:

• (3=8)r5c2-(8)r6c12=(8)r6c4-(8=pair13)r4c4,r5c5-(3=7)r4c5-(7)r8c5=(7)r8c123-(7=pair38)r75c2
• => sis: (3)r5c2=(3)r7c2 => r128c2≠3

As typically happens with this type of AIC, the illusion of using (3=8)r5c2 twice exists. This is again just a function of the limitations of the AIC notation. One can easily get this deduction using the counting method. The counting method is, in my opinion, more start point independent. What I mean by this is that one could start the count with any of the strong inference sets considered. Just for kicks, let us start the count somewhere in the middle:

1. (7)r8c123=(7)r8c5. One row, two columns. +1
2. (73)r4c5. +0
3. (31)r5c5. +0
4. (318)r4c4. +0
5. (8)r6c4=(8)r6c12. +0
6. (83)r5c2. +0
7. (837)r7c2. +0. Note by default we had placed 7's in the result column, and the eights are not interacting
8. At this point, the mental matrix can be column shuffled.
9. Move the sevens over out of result column. Place (3)r57c2 in column 1.
10. Place (8)r57c2 in column 2. Let arguments 1-5 above follow. (-1). total zero.
11. sis: [(3): r5c2,r7c2] => r128c2≠3

Note that no real knowledge of ALS was required to make the counting work. This is perhaps a concern, as it removes all feel of elegance from the deduction. Nevertheless, knowledge of how ALS work certainly makes this deduction much easier to find.

Step 3e - Hidden triple 134 - or the conjugate naked quad 2569

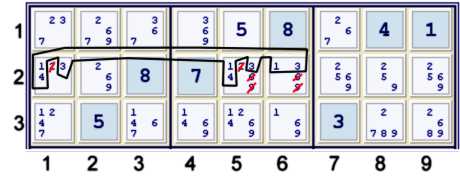
The elimination of 3 from r2c2 reveals

• Hidden triple 134 r2c156 => r2c156≠269
• => (2)r3c5 %box&column, thus UP 27

Step 4a - simple coloring

At this point, there are many deductions possible. Some are complex. Some less complex. Unfortunately, one will need a complex one sooner or later. I suppose I decided to use a fairly complex one next. I think this puzzle warrants the complexity.

Step 4b prelude - An Almost Y Wing Style

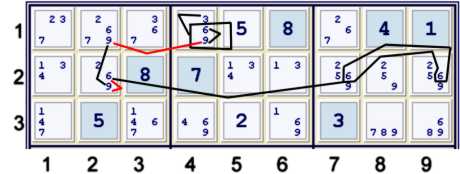
One can often use Almost Y Wing Styles to help find a place to search. Above, but for candidate 3 at r4c1, one would have:

• (6)r79c2=(6-9)r2c2=(9)r1c2-(9=6)r1c4
• Since this almost Y Wing style has a potential target, it may be worth investigating
• Note further that we have an Almost Almost naked pair 36 at r1c34.
• The Almost Y Wing style serves to reduce this Almost Almost naked pair from 2 degrees of freedom to just one.
• Thus, if we can find that (3)r4c1-(7)r3c1, then the potential target (6) at r1c7 is eliminated.

There are literally dozens of ways to finish this chain. Several of them are equivalent in complexity. Some use AUR 59 r25c78. Some use Kraken row 7's in row 1. Some are basically conjugate with each other. The one I prefer follows.

Step 4b A Festival of Almosting

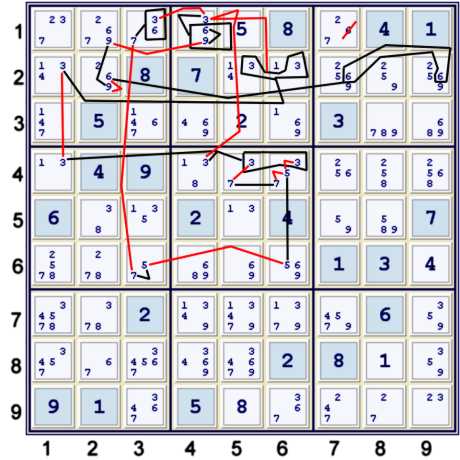
Above, find a deduction that does not transparently represent as an AIC. Noting the clues explained in the prelude, the following count can be undertaken:

1. (6)r2c79=(6)r2c2. +1
2. (9)r2c2=(9)r1c2. +0
3. (693)r4c1. Place 6 in result column. +0. (note one could be more general and place the 6 there later)
4. (637)r3c1. Place 6 in result column. +0. (same note applies, this line would be +0 regardless)
5. (75)r6c3. +0
6. (5)r6c6=(5)r4c6. +0
7. (7)r4c6=(7)r4c5. +0
8. (3):[r4c4,r4c6,r4c5,r4c1]. note only r4c1 is unlinked. +0
9. (3)r2c1=(3)r2c56. Both threes are linked.(-1). Total zero.
10. => sis [(6): r1c34=r2c79] => r1c7≠6

This deduction is a bit longer than I prefer - depth 9. I believe a max depth 8 solution is possible for this puzzle. However, the one I found used twice as many total steps and actually rated more poorly in spite of less depth. Of course, that is relevant only to my rather unusual rating system.

The elimination of this 6 seems, at first, to be rather uninspiring. In fact, the puzzle is now significantly undone. I find it interesting that r1c7 is again the focus of a significant elimination.

Just for kicks, here is how I see this elimination thinking in terms of AIC:

• (Y Wing Style 69=3)r2c279,r1c2,r4c1-(finned X Wing 3)r24=(hidden pair 37-5)r4c56
• =(5)r6c6-(5=7)r6c3-(7=pair36=9)r1c34-(9)r1c2=(9-6)r2c2=(6)r2c79
• => sis[(6)r2c79,(6)r1c4,(pair 36)r1c34,(6)r2c79] => r1c7≠6

As I noted, the AIC representation lacks some clarity. I may append this page with the appropriate matrix representation later.

When I search for a deduction, I tend to count in groups rather than individual arguments. This makes the deductions much easier to find. To wit:

1. (6)r2c79=r2c2. +0
2. (9)r2c2=r1c2. +0
3. (pair36=9=7)r1c34. Temporarily, perhaps, place sixes in result column. +0
4. (75)r6c3 +0
5. (5)r6c6=(HP57)r4c56 +0
6. (HP37)r4c56=(Finned X wing 3)r4c41,r2c156 -1. total zero.
7. Leave all sixes in result column
8. sis:[(6): r1c34,r2c79] => r1c7≠6

This concludes the second page of this solution. Eventually, the link to the next page will gain validity.