Tough Sudoku Proof for March 1, 2007

The following is an illustrated proof for the Tough Sudoku of March 01, 2007. There are many ways to tackle this one. The primary focus of this page is to illustrate using Forbidding Chains, also called Alternating Inference Chains or AIC.

You may need to refer to previous blog pages to understand this proof. Links to these pages are found to the right, under Sudoku Techniques.

At many times during this illustration, there are other steps available. It is not the goal of this page to show every possible step, but rather to illustrate steps that, taken together, unlock this puzzle

The information on the following blog pages is required to understand this page:

• Forbidding Chains 101 The Theory
• Locked Candidates
• Pairs, Triples, Quads. Please note that finding Hidden Pairs is discussed at some length in the series of Easy Proofs done in February.
• Forbidding Chains 102 The Practice to find the chains
• Y wing styles
• Finding Y wing styles
• Definitions: If a term is used on this page that you do not understand, the definition is likely here!

The illustrations of forbidding chains used on this blog page will share the same key:

• black lines = strong links
• red lines = weak links
• candidates crossed out in red = candidates proven false

Many steps that are possible will not be shown to keep the page as short as possible. However, every step that is shown can be justified by considering only the previous illustrated steps.

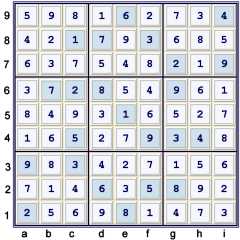
Puzzle at start

Hidden Pair 29 at UP 28

Hidden Pair 49 at UP 29

Editors note: I found the hidden pair 35 at d5e6 first, considering f2=5, f8=3. One only needs the locked 4's then at bc5 to get the listed cell solutions, as f6=4% box and then f5=6% box. The full hidden pair 49 is listed above, as it is required to make a later step.

If you prefer to enter the possibilities first, you can get to the same points using naked sets. Nevertheless, finding hidden pairs is often easier if you ignore the possibility matrix.

Puzzle at UP 31 - Another Hidden Pair

There have been many hidden pairs using candidate nine so far. Oftentimes, puzzles follow a pattern of one candidate being an early key to further eliminations. At this point, if one fills in the possibility matrix, the following steps are available, but not required for this proof: In order to follow this proof, one needs none of these steps.

• Locked 1's at ab2 forbids hi2=1
• fc on 1's: g9 == g3 -- d3 == d79 forbids f9=1
• Locked 2's at ef3 forbids hi3=2
• Locked 3's at h79 forbids h12=3
• Locked 3's at a56 forbids a79=3
• Locked 5's at ghi8 forbids gh9,h7=5
• Locked 6's at ab7 forbids h7=6
• Locked 7's at ac2 forbids hi2=7

Ignoring these steps is ok. Using these steps is also ok. In either event, one can continue as follows.

Puzzle at UP 32 - Locked candidate 8 - twice

One could perform all the listed eliminations on 8s with one step

• X wing on 8's at cf79 => ah79≠8

At this point in the puzzle, in my opinion, forbidding chains or something equivalent to them become a requirement for further progress. The standard puzzle mark-up revealed in Forbidding Chains 102, The Practice will indicate a number of potential areas to investigate for such chains. Since the 9s have been very active so far, and since a few of them exist in cells containing two circles in the puzzle mark-up, it should not be hard to find the following Y wing style chain.

Puzzle at 32 cells solved - Y wing style chain

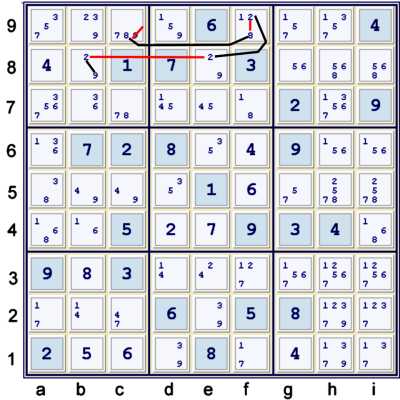
Illustrated above is the following Y wing style as a forbidding chain:

• c9=8 == f9=8 -- f9=2 == e8=2 -- b8=2 == b8=9 => c9≠9

Please note that there is no reason that the relationship between e8=2 and b8=2 be called only strong. It is both strong and weak. Strong and weak need not be mutually exclusive properties. In this case, it is the forbidding nature of their relationship that is required in the chain. One could always call a weak link a forbidding link. Perhaps that nomenclature is less confusing.

Using logic closer in style to a forcing chain:

• c9=8 => c9≠9
• c9≠8 => f9=8 => f9≠2 => e8=2 => b8≠2 => b8=9 => c9≠9

Using Y wing style logic: (centering on the vertex)

• f9=2 => f9≠8 => c9=8
• e8=2 => b8≠2 => b8=9
• c9=8 & b8=9 both => c9≠9

Using this elimination, one can solve a few more cells using cascading Unique Possibilities:

• c5 = 9% column
• b5=4, b2=1, a2=7, c2=4, b4=6, b7=3, a9=5, a7=6 all % cell
• h9 = 3% row & box

Puzzle at 42 cells solved - UP 42

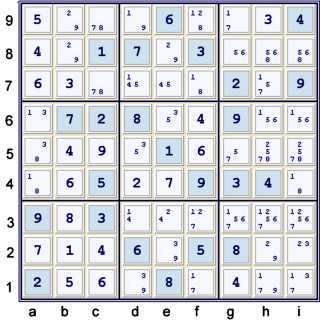
At this point, the puzzle mark-up will reveal almost too much information. This is not a failure of the mark-up, but rather indicates that almost everywhere one searches, there will be fruitful chains. I am ignoring the following additional steps, as I do not need them in my proof. Use of these steps will neither help nor hinder one in following the rest of this page.

• Hidden pair 45 at de7 forbids d7=1, h7=5
• X wing on 1's at dg39 forbids fhi3, f9=1

There are many paths to take here. I will illustrate one path that focuses primarily now on 1s. Although I have chosen not to execute the steps above in my illustration, those steps indicate to me that the 1s are perhaps almost begging to unlock the puzzle.

Another Y wing style chain

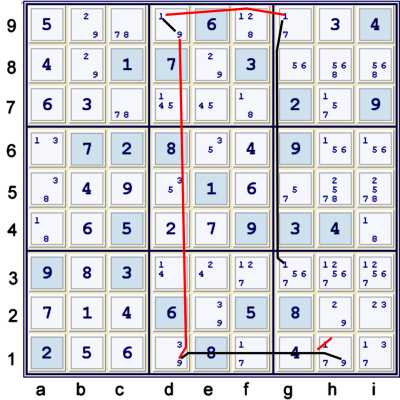
Illustrated above is a typical Y wing style chain using cell d9=19 as the vertex. Again, it is perfectly ok that d1=9 == d9=9 and d1=9 -- d9=9. The chain requires only the latter:

• h1=9 == d1=9 -- d9=9 == d9=1 -- g9=1 == g3=1 => h1≠1

It is very common that a cell limited to exactly two values forms a bridge between two candidates in a chain. This same concept is used again in a slightly longer chain:

Forbidding Chain (AIC) using four strong sets

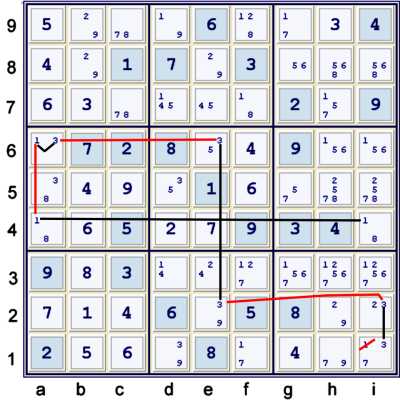
Above, the cell a6=13 acts as a bridge between 1s and 3s. Again, note that native strong sets are also weak, and that the chain uses whichever relationship is required:

• i1=3 == i2=3 -- e2=3 == e6=3 -- a6=3 == a6=1 -- a4=1 == i4=1 => i1≠1

Basically, the chain can be read either left to right, or right to left (all properly written forbidding chains can be read in both directions). Reading left to right, the chain says:

• i1=3 or
• i1≠3 => .... => i4=1

Reading right to left, the chain says:

• i4=1 or
• i4≠1 => .... => i1=3

No matter which way one reads it, at least one of {i4=1, i1=3} must be true, and both {i4=1, i1=3} => i1≠1. This is precisely the same as saying:

• i4=1 == i1=3 => i1≠1

Starting now with f1=1% row, the puzzle is easily solved using cascading Unique Possibilities, all of which are % cell (naked singles).

Solved Puzzle

Proof

1. Start at 23 filled - the given puzzle. Unique Possibilities to 28 filled. (UP 28).
2. Hidden pair 29 at be8 forbids b8=46, e8=45 UP 29
3. Hidden pair 49 at bc5 forbids df5=4, b5=36, c5=8 UP 31
4. Hidden pair 39 at d1e2 forbids d1=14, e2=24 UP 32
5. 1. Locked 8's at hi8 forbids h79=8
   2. Locked 8's at a45 forbids a79=8
   3. Y wing style: c9=8 == f9=8 -- f9=2 == e8=2 -- e8=9 == b8=9 forbids c9=9 UP 42
6. 1. Y wing style: h1=9 == d1=9 -- d9=9 == d9=1 -- g9=1 == g3=1 forbids h1=1
   2. i4=1 == a4=1 -- a6=1 == a6=3 -- e6=3 == e2=3 -- i2=3 == i1=3 forbids i1=1 UP 81

• Sets: 3(2) + 2(1) + 3 + 3 + 4 = 18
• Max depth 4 at step 6.2
• Rating: 2(.01) + 3(.03) + 2(.07) + .15 = .40