The following is an illustrated proof for the
Tough Sudoku of March 26, 2007.
This puzzle is fairly tough.
You may need to refer to previous blog pages to understand
this proof. Links to these pages are found to the right, under Sudoku Techniques.
At many times during this illustration, there are other steps available. It is not the goal
of this page to show every possible step, but rather to illustrate steps that, taken together,
unlock this puzzle.
To understand this page, some previous blog pages that could be particularly helpful are:
The illustrations of forbidding chains used in this proof will share the same key:
- black line = strong inference performed upon a set (strong link)
- red line = weak inference performed upon a set (weak link)
- black containers define either:
- a multi-native strong set Boolean
- a grouping of a native strong set
- candidates crossed out in red = candidates proven false
Strong and weak need not be mutually exclusive properties.
Puzzle at start
A few Unique Possibilities are available here. All of them are hidden singles:
Hidden Pairs
Without considering the possibility matrix, one can locate some hidden pairs:
- a9c7 = 79
- gh8 = 23
- cf4 = 68
Naked Pair 79
The naked pair 79 at a49 =>
a135≠79
Coloring with 9s - Finned X wing
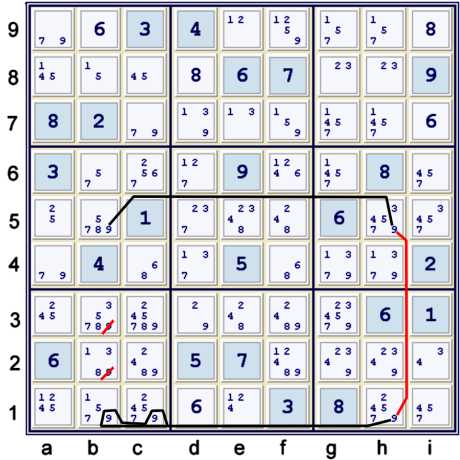
Above,the 9s in rows 1 and 5 form a short forbidding chain on 5s:
- b5 == h5 -- h1 == bc1 => b23≠9
Although I do not illustrate it, nor is it required to solve the puzzle, there is also
a short forbidding chain on 8s available here:
- c4 == f4 -- e5 == e3 => c3≠8
Y wing Style with 138
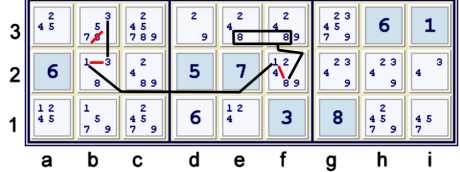
Using the 1s at bf2 as a vertex:
- b2=1 => b2≠3 => b3=3 => b3≠8
- f2=1 => f2≠8 => ef3 contains 8 => b3≠8
As a forbidding chain:
- b3=3 == b2=3 -- b2=1 == f2=1 -- f2=8 == ef3=8 => b3≠8
Typical Forbidding Chain using 4 strong inferences
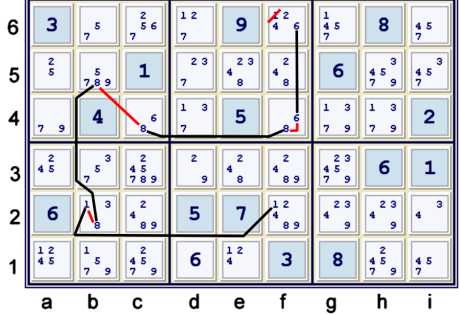
Above, the following chain, newly available after the Y Wing Style, is illustrated:
- f2=1 == b2=1 -- b2=8 == b5=8 -- c4=8 == f4=8 -- f4=6 == f6=6 => f6≠1
Although some of the weak inferences shown above are also strong, the chain requires the inferences
that are illustrated.
If you have trouble following this step, one can also use a proof by contradiction, although
it is not required:
- Suppose f6=1 =>
- f6≠6 and f2≠1 =>
- f4=6 and b2=1 =>
- c4≠6 and b2≠8 =>
- c4 = b5 = 8, which is not allowed!
Almost Locked Set used in a chain
Illustrated to the left,
- d3=2 == d3=9 -- d7=9 == {pair 13 at de7} -- e9=1 == e9=2
- => d13≠2
Also possible, but not illustrated,
- d3=2 == d3=9 -- d7=9 =={hidden pair 59 at f79} -- f9=2 == e9=2
- => d13≠2
Although the latter may be harder to see, one can see that since:
- f7=5 == f9=5,
- f79 = Hidden pair 5x
- where x is one of 1,9,2
Knowing that we always have such a almost hidden pair anytime one candidate is limited to two
locations in a container is sometimes valuable. Generally, it indicates possible ALS, either hidden
or naked, or both, plausibility.
The step
This step uses the Almost Hidden Pair 15 at f79:
- f2=1 == {Hidden pair 15 at f79} -- f9=9 == a9=9 -- a4=9 == b5=9 -- b5=8 == b2=8
- => b2 ≠1
If one has trouble with this one, consider what if:
- b2=1 => b2≠8 & f2≠1
- => b5=8 & f79=Hidden pair 15
- => b5≠9 & f9≠9
- =>a4 = a9 = 9
After b2≠1,
- f2=1 (only 1 in row)
- e1=4 (naked single)
- e3=8 (naked single)
Easy four strong inference chain
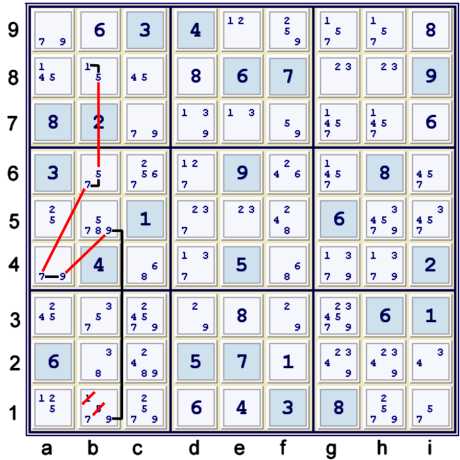
Above, the following chain is illustrated:
- b1=9 == b5=9 -- a4=9 == a4=7 -- b6=7 == b6=5 -- b8=5 == b8=1 =>
- b1≠1, as b8=1 == b1=9
- b1≠5, as b6=5 == b1=9
This chain is a good example of a typical Y Wing Style getting an added strong inference to get
the original elimination plus one more. In other words, the chain:
- b1=9 == b5=9 -- a4=9 == a4=7 -- b6=7 == b6=5 => b1≠5
- and we just add one each of a strong and weak inference:
- ...-- a8=5 == a8=1 => b1≠1
Not illustrated, Locked 2s at df3 => acg3≠2. The puzzle then cascades with
Unique possibilities
until 53 cells are solved.
Coloring using candidate 7
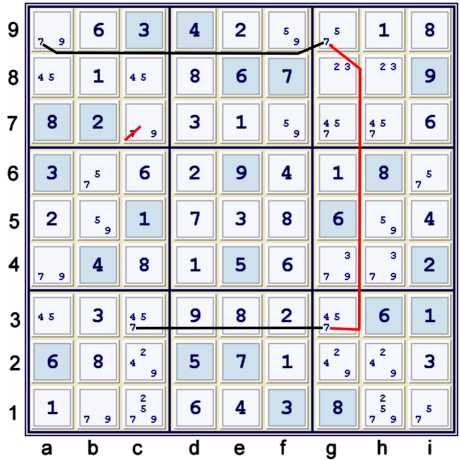
Above, an easy coloring elimination with candidate 7 unlocks the puzzle. One could write:
- fc on 7s: c3 == g3 -- g9 == a9 => c7≠7
Proof
- Start at 22 filled - the given puzzle. Unique Possibilities to 27 filled. (UP 27).
- Hidden pair 79 at a9c7 forbids a9=15, c7=45
- Hidden pair 68 at cf4 forbids c4=79 and f4=1
- Naked pair 79 at a49 forbids a135=79
- fc on 9s: b5 == h5 -- h1 == bc1 forbids b23=9
- Y wing style: bc2=8 == f2=8 -- f1=1 == b2=1 -- b2=3 == b3=3 forbids b3=8
- f2=1 == b2=1 -- b2=8 == b5=8 -- c4=8 == f4=8 -- f4=6 == f6=6 forbids f6=1
- d3=2 == d3=9 -- d7=9 == pair 13 at de7 -- e9=1 == e9=2 forbids e13=2
- f2=1 == hp15 at f79 -- f9=9 == a9=9 -- a4=9 == b5=9 -- b5=8 == b2=8 forbids b2=1 UP 30
- Locked 2s at df3 forbids acg3=2
- b8=1 == b8=5 -- b6=5 == b6=7 -- a4=7 == a4=9 -- b5=9 == b1=9 forbids b1=15 UP 53
- fc on 7s: c3 == g3 -- g9 == a9 forbids c7=7 UP 81
- Sets: 1 + 5(2) + 3 + 3(4) + 5 = 31
- Max depth 5 at step 2.8
- Rating: .01 + 5(.03) + .07 + 3(.15) + .31 = .99
Suitably tough!