The following is page two of an illustrated proof for the
sudoku.com.au tough puzzle of 01/30/08.
Page one is richly detailed with specific information
on how I found deductions. This page will continue with similar specific analysis.
Previous blog pages may be helpful. Links to these pages are found to the right,
under Sudoku Techniques. I may later list specific pages.
The illustrations of steps shown on this page will share this key:
- black line = strong inference performed upon a set (strong link)
- red line = weak inference performed upon a set (weak link)
- black containers define a partioning of a strong set(s)
- candidates crossed out in red = candidates proven false
- boxes highlight some groups
Please be aware that, for me,
strong and weak need not be mutually exclusive properties.
Mark-Up
Generally, I keep the original puzzle mark-up and update it - at least until I spill coffee on it. Below, the first
mark-up has been updated with the new information. Not much changed. Three candidates have been crossed out, and
(2)g7 has been underlined to reflect: (2)g7=(2)de7.

An ALS - AAIC Digression
Below, a short digression in how one can use thinking shortcuts to help analyze any puzzle. The graphic below
is of an actual Almost Locked Set ALS in this puzzle, but the information is not puzzle specific.
To the left, the ALS(1369)f389 is highlit. An ALS is a group of cells within a large container, in this case
a column, such that (n+1)candidates exist in (n)cells. In this case, (4)candidates exist in (3)cells. This situation
always constrains the possible puzzle solutions. Thus, it has some power. The constraint is fairly trivial:
- Of the (n+1) candidates, at least (n) must exist within the (n) cells.
- In this case, 4 choose 3 of (1369) must exist at f389
This situation immediately provides a multitude of deduced strong inference sets. The most useful of these deduced
sis are generally those that are the most restricted. Thus, in this case, (1)f38=(6)f9 would be the most likely
useful sis derived from the ALS. There are many ways to prove this relationship. One may, upon inspection, say that
(pair39)f389 is impossible, thus (1)f38=(6)f9 must be true. One could build a small matrix:
The matrix above is a pigeonhole matrix. The result column gives the result: sis:[(1)f3,(1)f8,(6)f9]. There is no
requirement to use such an animal, but it is instructive. One could also write the AIC:
- (1)f38=(pair39)f38-(39=6)f9
Note the AIC loses some of the apparent symmetry. This does not reflect upon reversibility. It merely reflects
upon a minor problem with nomenclature. One could write the shorter AIC:
The extension of ALS to AAIC is very easy. For each AAIC, there exists a
Mixed Block Matrix such that
any arbitrary sis that exists from the sis under consideration can be proven. MBM, by their nature, are completely
reversible. Always. End of digression...
Another Digression
Above, one may wish to note: (6)f9=(Hidden triple568)f156. Thus one has an Almost Hidden Set (AHS).
One could say:
- ALS(1369)f389 is conjugate with AHS(568)f1569
Such conjugate relationships always exist with Almost sets, just as they always exist with actual zero degree of freedom
sets. It is useful to be aware of this conjugacy. It implies a specific partitioning of derived sis within the puzzle.
The same conjugacy exists for every derived sis, including those from AAIC. It is less apparent. It must exist. Formally, one could say:
- For each MBM that proves a sis, there exists
- an MBM using only conjugate sis that proves the same sis
Awareness of this conjugacy seems less useful. I hope someday to use this conjugacy in conjunction with Uniqueness to develop
some interesting theorems. This conjugacy, in my opinion, is the basis for many other techniques, including
Pattern Overlay Method (POM). Regarding uniqueness, it says something about the number of solutions in any possible
partitioning of the puzzle. End of second digression...
Back to the actual puzzle!
Step 2e - An almost finned Jellyfish
Illustrated below is an elimination that I found to be very appealing. I am not certain about the precise name
that should be ascribed to the emergent sea creature below, but regardless of the species, 'tis profoundly beautiful to me.
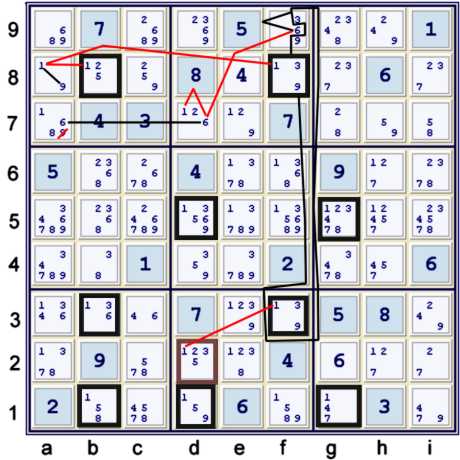
Above, a relatively simple relationship is graphed. Consider both:
- (6)a7=(6-1)d7
- (6)a7=(6)d7-(6)f9=(triple139)f389 => (6)a7=(1)f38
Therefor, if you prefer,
- (6)a7=(6)d7-(1)d7,f156
- =[(1)Finned Column Jellyfish using: b138,d125,f38,g15]
- Alternatively, find the finned row swordfish and add f3=f8
- -(1=9)a8
- =>(6)a7=(9)a8 => a7≠9
(1)d2 is the fin to the Almost Jellyfish, and clearly:
- (1):[f8=f3-d2=[Jellyfish @ b138,d15,f38,g15]-(1)a8
You may wish to note that this particular Almost Finnned Jellyfish can be broken down into
Xwing-like components. For reference,
one can easily build a matrix representation of this step. Note, however, how the matrix tends to detract from the visual
elegance of the pattern (in my opinion, anyway). The matrix below is MBM, with the symmetric pigeonhole matrix block
in
bold. Aside from that partition, the matrix defaults to Triangular.
| 6r7 |
a7 |
d7 |
|
|
|
|
|
|
| a8 |
9 | | 1 | |
| | | |
| f8 |
| | 1 | 3 |
9 | | | |
| f9 |
| 6 | | 3 |
9 | | | |
| f3 |
| | | 3 |
9 | 1 | | |
| 1b |
| | b8 | |
| b3 | b1 | |
| 1g |
| | | |
| | g1 | g5 |
| 1d |
| d7 | | |
| d12 | | d5 |
What I like about the matrix representation is that it dispenses with the illusion that one need
to consider any sis in this deduction more than once. Also, the conclusion of (9)a8=(6)a7 is very clear.
Step 2f prelude
With step 2e, three updates are made.
- a7≠9 updates the Possibility Matrix.
- My mark-up is changed to reflect not only a7≠9, but also (9)e7=(9)h7. Thus,
- (9)e7 is circled
- (9)h7 is circled again
- (6)a7=(9)a8 updates all possible solutions to this puzzle.
- Specifically, in my mind, (6=9)a78 is emblazened
This seems modest, but instead is very useful. It seems silly not to remember such a simple piece of information.
Step 2f Two ALS linked
The following step is an immediate and, for this puzzle, trivial, result of the previous step.

Above, the following chain is graphed, using (6=9)a78:
- (8=2)g7-(2)de7=(2)d9-(2)c9=(triple689)ac9,a78 =>
- (8)g7=(8)ac9 => a7,g9≠8
Finding this chain is the natural result of being aware of what step
2e truly means. It means, in this case,
that one had established the ALS(2689)ac9,a78 where a78 is a grouped argument (super cell, if you will) containing (6=9).
Step 2g Prelude 1
On the previous page, the AAIC below was partially noted. With the newly stronger candidate 9 in row 7, the
AAIC below becomes an Almost Proving Loop. An almost proving loop merely Almost asserts a singularity, whether it
be grouped or not, within a sis.

Above, given step 2c, it is fairly obvious that (1)f8=(9)h7 using:
- (1)f8=[(9)h7=(9-4)h9=(4-3)g9=(3)df9-(3=9)f8]-(9)e7=(9)h7
Such a chain snippet is stored in my head as (1)f8=(9)h7 because this is more concise - and more easily linked - than
(1)f8=(12)e7. There really is no reason, theoretically, to prefer one over the other.
Step 2g Prelude 2
Given the ALS: (3)e8=(pair19)af8, and given the fact that (19)f8=(39)f8 is always true when f8 is limited to 139,
the next chain snippet became functionally significant.
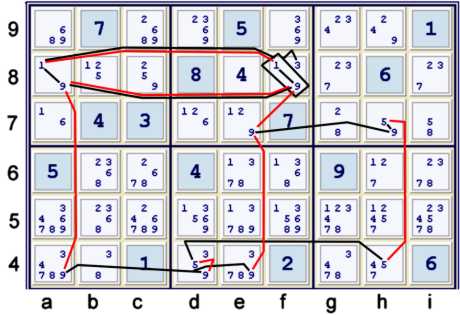
Above, find another Almost Proving Loop. This one has the illusion of having an extra degree of freedom, but it does
not. Graphed above, find:
- (3)f8=(pair19)af8
- Thus mentally, conclude (3)f8=(9)af8
- Note the almost proving loop using candidate 9
- (9=5)h7-(5)h4=(5-9)d4=[[(9):h7=e7-f8=a8-a4=e5-e7=h7]=(3)f8]
- => (3)f8=(9)h7
The two preludes combine:
- (9)h7=(3-1)f8=(9)h7
=>
- (9)h7 %AIC
Whenever one can assert a value using AIC, one can reduce depth (number of sis considered) by 1 and prove a
conjugate group of eliminations. Thus, one could rewrite the deduced truth as shown below.
Step 2g
Below, find an attempt to illustrate h7≠5.

One can write the elimination shown above in many ways as AIC. The choice of how to partition the sis is
fairly arbitrary. All will focus upon both the Kraken cell (139)f8 and the Kraken row (9)ade5 to determine the partitions.
In many ways, this step is similar, conceptually, to both steps 2d and 2c which involved some of the same sis.
Often, I forge ahead in a puzzle beating upon the same restrictions multiple times. Below, find the matrix representation
of the elimination proof. In this case, a Triangular Matrix does the job.
| 5r4 |
h4 |
d4 |
|
|
|
|
|
|
| 9r7 |
h7 | | e7 | |
| | | |
| 9r4 |
| d4 | e4 | a4 |
| | | |
| a8 |
| | | 9 |
1 | | | |
| f8 |
| | 9 | |
1 | 3 | | |
| 3r9 |
| | | |
| df9 | g9 | |
| 4r9 |
| | | |
| | g9 | h9 |
| 9h |
h7 | | | |
| | | h9 |
Note the conclusion:(9)h7=(5)h4 => h7≠5. The real key to this one, in my opinion, is the recognition of
(5)d4-(9)d4.
One can now solve some cells:
- (9)h7% cell
- (5)i7% box and row
- (8)g7% box and row
Thus, UP 27.
The slow, tortured process of blogging the tangled mess of my mind regarding this sudoku puzzle will continue on
page three.