Welcome back!
This proof is multi-page and multi-faceted. Hopefully, you have already digested the
First Page.
This page contains a few interesting ideas for study. All of them are the natural result of
viewing Forbidding Chains or Alternating Inference Chains (AIC)
not only with strict precision, but also with an open mind about possible relationships.
Before I once again venture into the truly interesting stuff, first I must dispense with
some rather mundane chains. Nevertheless, understanding of the interesting chains can only
be achieved after first mastering the relatively easy concepts/chains.
A typical Four Strong Set Chain using candidates 1589 and strength in location
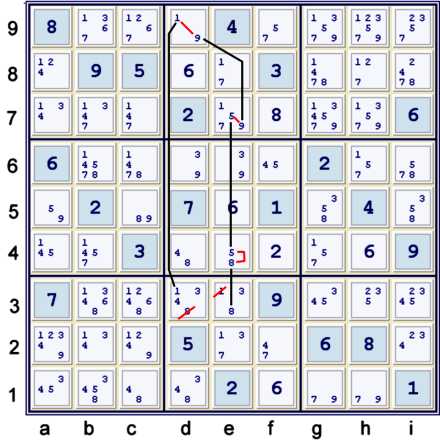
Illustrated above, a chain that is heavily indicated by the standard puzzle mark-up should
be easy to find. Perhaps the only fun thing about this particular chain is that the endpoints
of the chain allow two eliminations, as shown. Here is the chain, written in my usual outdated
style:
- d3=1 == d9=1 -- d9=9 == e7=9 -- e7=5 == e4=5 -- e4=8 == e3=8
- => d3=1 == e3=8 => d3≠8 & e3≠1
Although the chain above is perhaps mundane, here is what I think after making these eliminations:
- d3=1 == e3=8 act very much like a single cell limited to only 1,8
- But for d3=1 -- e3=8, I could treat the relationship above precisely like a single
super cell in row 3 and in box e2
- This tidbit of information will be stored in my head for the rest of the puzzle
- It maybe useless information, it maybe useful - that I do not know at this point!
- e7=59 == e7=17 is an interesting relationship. Now even more so. Note: I have a crossing
point of Almost pair 17 in column e with Almost Hidden Pair 59 in row 7
- Again, I have no clue how valuable this information may be, but it is now also somewhat
cross referenced with an almost super cell 18 in row 3
Hopefully, this window into my head is helpful. The general goal of how to find complex chains
less painfully is the prize!
A typical Y Wing Style using candidates 48
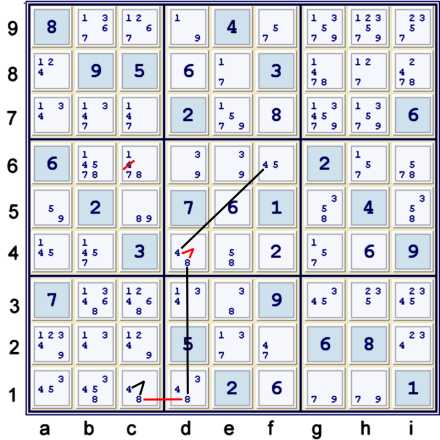
If you have been paying attention to my previous blogs that have placed much emphasis on
Y Wing Styles, then the chain illustrated above should be easy to find. c1=48 and d4=48
are common markers for a very common Y wing style. Sadly, that type of Y wing style is not
found here. Nevertheless, one should look for it. By looking for that type of Y wing style, the
one illustrated above:
- c1=4 == c1=8 -- d1=8 == d4=8 -- d4=4 == f6=4 => c6≠4
can become easy to locate.
Almost Almost hidden pair 58 - the concept visualized
Illustrated to the left is a chain snippet:
- {Hidden pair 58 at b16} == {b3=8 == b4=5}
You may consider the logic involved in many ways. One way is to consider that:
- ~{b3=8 == b4=5}
- => b3≠8 and b4≠5
- => Hidden pair 58 at b16
So we have concluded:
- ~{b3=8 == b4=5} => {Hidden pair 58 at b16}
However,
- A => B is equivalent to
- ~A OR B
- Also written as ~A == B
- Thus ~A => B can be written as: A == B
Putting this all together: (substituting for A,B above)
- {b3=8 == b4=5} == {Hidden pair 58 at b16}
There is no reason to repeat this exercise everytime one sees this type of Almost Almost Hidden
Pair configuration. One can immediately know, from previous analysis, that this relationship
exists. I am aware that using ~ in an argument is viewed with disdain in some sudoku circles.
To this I say the following: One needs never do it again, as the concept has been proven in general!
Thus, the relationship becomes visual for every possible occurennce, as it has been proven sound
in general. This is the power of mathematics and logic: Prove general truths, then use them over
and over again. No need to reinvent the wheel for each wheeled conveyance!
To me, this is a powerful concept, as now I can use this conceptual relationship in a chain. What
I have derived is a chain snippet, or piece of a chain. It is of the general form, using Booleans, of
A == B, so it looks an awful lot like part of an AIC, or Forbidding Chain. More precisely,
it is exactly a valid AIC. Thus, it is also a valid AIC link in any larger AIC chain.
Below, find how I use this piece of information in a larger chain
A wrap around chain with an internal discontinuity
Alternatively, an extended Hub plus a simple Hub connected to an ALS Rim
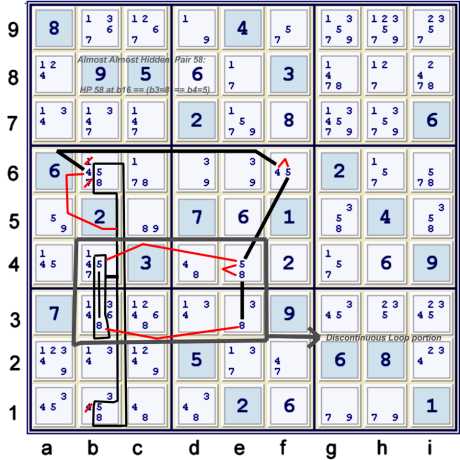
Illustrated above, we have an interesting (to me anyway) group of connected chains:
- {Hidden pair 58 at b16} == {b4=5 == b3=8}
- f6=5 == e4=5 -- e4=8 == e3=8 -- b3=8 *==* b4=5 -- e4=5 == f6=5
- This chain above is marked with asterisks, as it almost exists, but does
not as b3=8 == b4=5 is not a native puzzle condition
- f6=5 -- f6=4 == b6=4
- This chain is not an AIC, but it is a valid piece of an AIC
Putting all of these pieces together, one has a very nice chain:
- {Hidden pair 58 at b161} == {b4=5 ==1b3=8 -- e3=8 == e4=8} -- e4=5 == f6=5 -- f6=4 == b6=4
- Since {Hidden pair 58 at b16} -- b6=4, we also have some sort of wrap-around,
or continuous chain. Unfortunately, most of the proven strong links do not forbid anything:
- {b4=5 == b3=8 -- d3=8 == d4=8} == e4=5 is too asymmetrical to have
much practical use.
- f6=5 == f6=4 could be useful, but we already have that!
- {Hidden pair 58 at b16} == b6=4
The reason that I have highlit the part of this chain that I find to be discontinuous is so that
one can clearly see that some of the weak links used are not proven strong. Thus, the following
weak links are not proven strong:
- b3=8 -- e3=8
- b4=5 -- e4=5
- e4=5 -- e4=8 (although we already have e4=5 == e5=8, that is irrelevant here!)
Finally, as it turns out, noticing that this chain is a continuous loop, or wrap around, is of
absolutely no use
for this puzzle. However, I thought it instructive to analyze completely what is actually
happening. A little knowledge can be a dangerous thing! In fact, if one erroneously were to conclude
that all the weak links shown here are indeed strong, then the puzzle would be accidently advanced.
In this case, only legal reductions would be made. They would be made, however, without justification.
PERHAPS too much information here?!!
Chain snippet digression
Non-native Almost Chain pieces, such as b3=8 *==*(almost)b4=5, are a very
valuable tool to include in one's toolbox. Recognizing such almost chain pieces becomes easier
with practice. Using such almost chain pieces can be a powerful technique to humanly solve
puzzles using logic. They often provide relationships that look odd, but are quite beautiful
to someone like me.
A typical depth 4 chain using 48
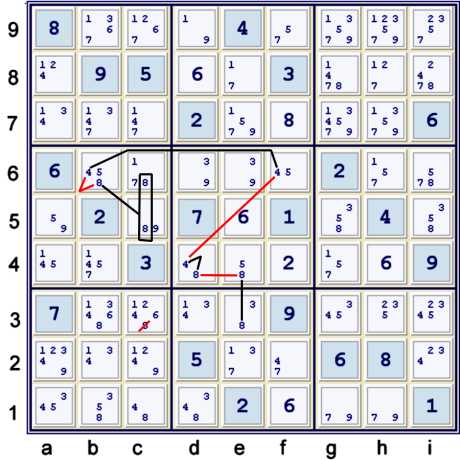
Illustrated above is a simple chain. The only interesting aspect is the grouped use of the
8s in box b5. Again, this pattern is heavily indicated by the standard puzzle mark-up. I choose to
insert this step here to give everyone a break from the previous step before venturing into
Almost land again. For the sake of completeness, here is the chain:
- c56=8 == b6=8 -- b6=4 == f6=4 -- d4=4 == d4=8 -- e4=8 == e3=8 => c3≠8
Of course, one can alternatively use the strong 5s in box e5 to establish d4=4 == e3=8.
Thus the same elimination can also be written:
- c56=8 == b6=8 -- b6=4 == f6=4 -- f6=5 == e4=5 -- e4=8 == e3=8 => c3≠8
Perhaps, I should have illustrated the step that way, since the overlap with the previous step is
then quite large. (Three out of four strong sets reused). Oftentimes, puzzles are unlocked
with mutliple uses of the same groupings of strong sets.
The Almost Y Style 17 from Page 1 used again in a chain
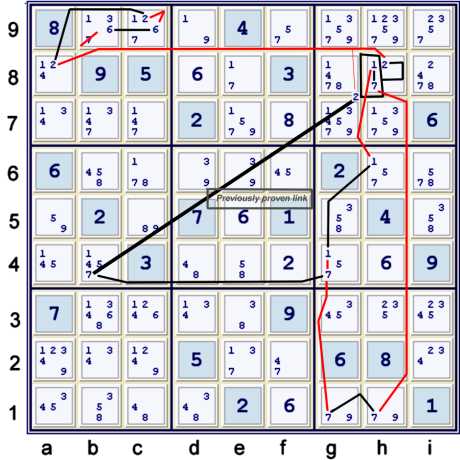
Previously, on the preceding page, the relationship: h8=2 == b4=7 was established. It is not
difficult to then use this relationship again for a slightly different chain. Illustrated above:
- b9=6 == c9=6 -- c9=2 == a8=2 -- h8=2 =={Previously detailed Y Style using 17} -- g4=7 == b4=7
This concludes the second page of this proof. There remains to be discussed not only some
very interesting steps but also some very neat ways to locate them. To further investigate
my absurdly grandiose road of soduku solving, kindly visit the
next page.