Solution Path for Tough Sudoku of May 25, 2009

The following illustrated solution for the Tough Sudoku of May 25, 2009 employs at least some steps of some interest, perhaps, to some. Although this sudoku can be solved without using the uniqueness deduction illustrated below, in my opinion the uniqueness deduction simplifies the solution.

This Sudoku probably solves with fewer steps. The steps chosen below are primarily for the purpose of teaching and illustration. I realize it is a bit grandiose of me to assume that I might do either well.

If this is your first visit to this blog, welcome! Unfortunately, if you are a first time visitor, this page may seem like it is written in a different language. Well, it is. Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. The earliest posts are at the bottom, and if you have never perused the intricacies of our special coded language here, you may wish to start close to beginning. Then again, you may just decide to jump in and have fun decoding! The collection of sudoku strategies and sudoku techniques used in this puzzle are previously described. If I were not so lazy, I could provide specific links.......

Many steps not illustrated are possible.

The Puzzle

For those whom do not wish to struggle through the illustrations, I have written the steps taken in this solution at the bottom of the page in sudoku.com.au notation.

The Puzzle at UP 28 Unique Possibilities to 28 given or solved cells

Step 2: A short AIC (Alternating Inference Chain) using candidates 5 & 6

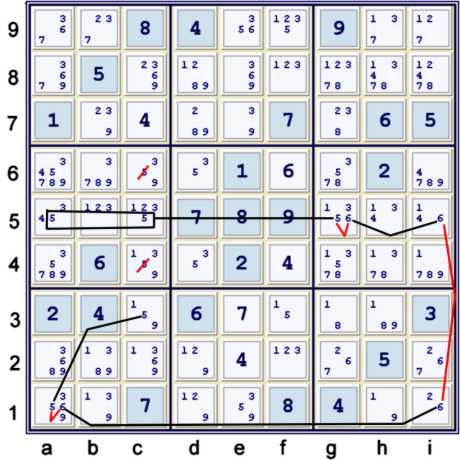
Above, I have illustrated a short AIC using candidates 5 & 6. The only difficult portion of this chain is using the grouping of candidate 5 at ac5. The type of puzzle mark-up that I prefer highlights this type of grouping, as I often find it useful. To highlight this group, I underline the 5 at g5, as it is the other end of the almost bilocal group. The chain could be written as:

• (5)ac5 = (5-6)g5 = (6)i5 - (6)i1 = (6-5)a1 = (5)c3 => c46≠5

One may note that many of the steps shown here could have been done in a different order, such as the next step.

Step 3: Another short AIC

This step could be seen easily, perhaps for some more easily, using mostly naked sets. Above, I have illustrated the following chain using hidden sets:

• (3)f2= (3-5)e1 = (5-6)a1 = (6-2)i1 = (2)d1 => f2≠2

Using mostly naked sets, one could find:

• (2)d1 = (nt139)bdh1 - (3)e1 = (3)f2 => f2≠2

Step 4: A continuous loop, or wrap-around chain, using candidates 2 & 5.

Short wrap-around chains such as the one illustrated below are my absolute favorite find while solving a sudoku. They illustrate the power of AIC's best, and avoid having to consider the same information multiple times to achieve multiple eliminations. But, enough with the inane preaching!

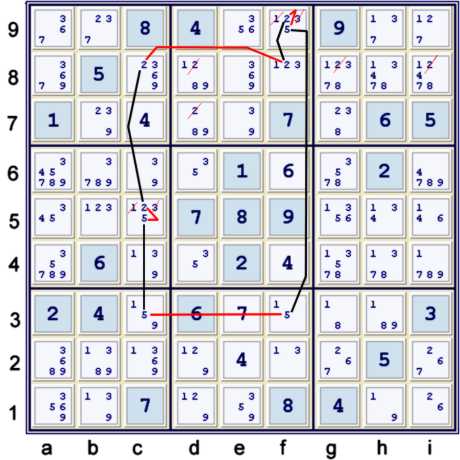
The first two steps have set up this step. The 2's at d78 above are eliminated because of the locked candidate (2) at f89, and normally would not be considered to be a result of such a chain. Please note that it matters not where one would start the following chain. Each potential starting point is completely arbitrary! I have been told many times by my wife that I am also completely arbitrary, but I think her meaning is slightly different.

• (5)c3 = (5-2)c5 = (2)c8 - (2)f8 = (2-5)f9 = (5)f3 loop =>
  1. (5=2)c5 => c5≠13
  2. (2)c8 = (2)f8 => gi8≠2
  3. (2=5)f9 => f9≠13
  4. (5)f3 = (5)c3 => nothing, as this is already a native condition of the current puzzle

Step 5: Another short chain that finally yields an elimination which allows some cells to be solved.

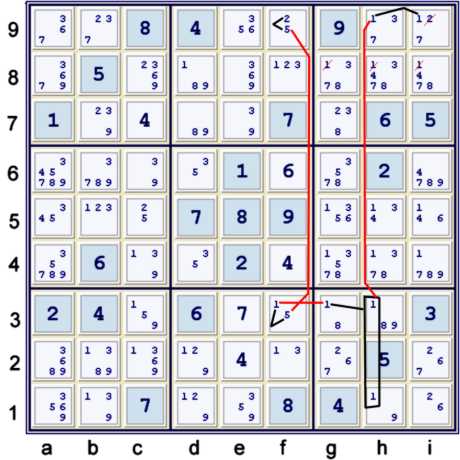
Usually, if one wishes to minimize the number of steps, steps that result in solving some cells are the quickest path. Oftentimes, however, the path has less to do with solving those cells, and more to do what is forbidden by the new cell solutions. This is precisely the case with the following step, which is powerful because it eventually eliminates (3) from g7. Here is the step:

• (2=5)f9 - (5=1)f3 - (1)g3 = (1)h13 - (1)h9 = (1)i9 =>
  1. i9≠2
  2. (2)g7 % box
  3. (8)d7 % row
• UP 30

My step 8 is available now. However, first I will dispense of a couple of other candidates to get more bang for the buck. Again, this is another one of those arbitrary decisions.

Step 6: A Ywing Style step using only hidden strengths

Step 7: Another Ywing Style, this time using a mixture of hidden and naked strengths.

• (5)e1 = (5-1)f3 = (1)gh3 - (1=9)h1 =>
• e1≠9

One could now use the locked 9's at d12. Doing so, or not doing so, will not matter after the next step.

Step 8: Uses a Almost Unique Rectangle Strong Inference Set in a chain.

The chain below is the longest chain of this solution. It has been available since 3 was removed from g7. Oftentimes, the use of hidden strengths in conjunction with a Uniqueness situation can be powerful, as illustrated below.

• The (AUR35) at dg46 =>
  • At least one of g46 is not (35) =>
  • At least one of these is true: [(3)g8, (35)g5] - note the grouping of (35)g5
• (3)g8 = (35-6)g5 = (6)g2 - (6)c2 = (6)c8 - (6)e8 = (np39)e78 =>
• f8 ≠3 =>
• A cascade of naked and hidden singles to UP 50

The grouping (35-6)g5 merely means that (3)g5 and/or (5)g5 are weakly linked, or forbid, or prevent, (6)g5.

Step 9: A naked pair

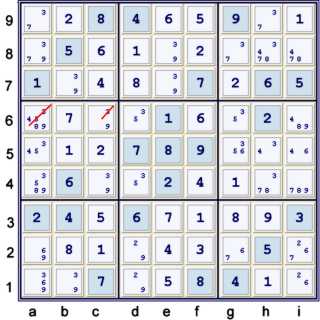
A lowly naked pair suffices to knock out the rest of this puzzle.

Solution

Solution steps

1. 1. Start 23, UP 28
   2. (np35)d46
   3. (nt189)g3h13
2. (5)ac5=(5-6)g5=i5-i1=(6-5)a1=(5)c3 => c46≠5
3. (3)f2=(3-5)e1=(5-6)a1=(6-2)i1=(2)d1 =>f2≠2
4. (2)f9=f8-c8=(2-5)c5=c3-f3=(5)f9 loop => d78.gi8≠2, c5.f9≠13
5. (2=5)f9-(5=1)f3-gh3=h1-h9=(1)i9 => ghi8≠1, i9≠2, UP 30
6. (1)c4=(1-2)b5=(2-5)c5=(5)c3 => c3≠1
7. (9)h1=h3-(9=5)c3-f3=(5)e1 => e1≠9
8. • (AUR35)dg46 => sis[(3)g8, (35)g5]
   • (3)g8=(35-6)g5=g2-c2=c8-(6)e8=(np39)e78 => f8≠3, UP 50
9. (np35)dg6 => ac6≠35, UP 81