Coloring Proof for March 31, 2007

The following is an illustrated proof for the Tough Sudoku of March 31, 2007. The most important technique employed on this page is Coloring. Coloring, as I use the term, means making an elimination by considering only 1 type of candidate.

You may wish to refer to previous blog pages to properly understand this proof. Links to these pages are found to the right, under Sudoku Techniques.

This page illustrates, in my opinion, the minimum number of deduced elimination steps that this puzzle requires to solve. Although many other steps are possible, they are not shown, as to show every possible step is prohibitive in both time and space!

The information on the following blog pages may be helpful:

• Locked Candidates
• Pairs, Triples, Quads.
• Coloring
• Finding Coloring
• Forbidding Chains 101 The Theory
• Definitions: If a term is used on this page that you do not understand, the definition is likely here!

The illustrations of forbidding chains used in this proof will share the same key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set
• candidates crossed out in red = candidates proven false

Strong and weak need not be mutually exclusive properties.

Puzzle at start

Although I prefer to search for Hidden sets at this time, the only hidden sets that I can find without entering the possibility matrix are hidden triples. Instead of using these, I shall use one of the naked sets that must exist in conjunction with each hidden set.

Naked Triple 134

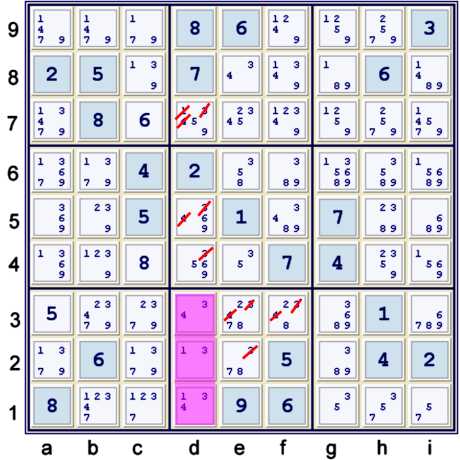
The cells:

• d1=134
• d2=13
• d3=34

Form a naked triple. Since this triple is completely contained in both of these houses:

1. column d
2. box e2

One can eliminate candidates 134 from the remainder of both column d and box e2, as shown.

After making these eliminations, one Unique Possibility is uncovered:

• f5 = 4% row & box

Locked candidate 8

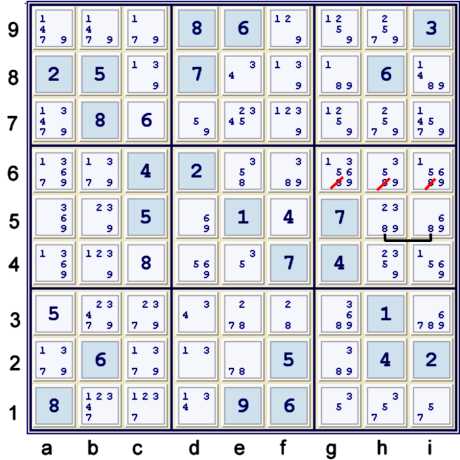
Although many locked candidate eliminations are available at this time, any one of three involving candidate 8 seems likely to solve the most cells. Illustrated above, since the 8s in row 5 are limited to cells h5 and i5, and since both those cells share the same box, 8s cannot exist in that box outside of row 5. This is because if they did, then there would be no 8s possible in row 5. This elimination can be written as a forbidding chain or Alternating Inference Chain (AIC) as:

• h5=8 == i5=8 => ghi6≠8

Also possible, and leading to the same eventual puzzle grid, are:

• Locked 8s at ef6 => ghi6≠8
• Locked 8s at h56 => gi6,i5≠8 (This one was available before the previous step)

After making any one of these three locked candidate eliminations with 8, the following Unique Possibilities cascade:

• h5=8 (hidden single, either in row or column, depending on which locked candidate elimination was taken)
• h4, b5, c1 = 2 (more hidden singles)
• a5, c8, e4, f7 = 3 (hidden singles)
• e8, i7, a9 = 4 (naked single and two hidden singles)

The puzzle now has 38 cells solved.

Possibility Matrix after UP 38

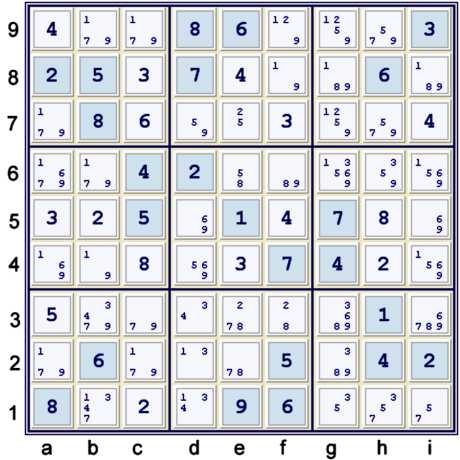
Again, there are many steps possible here. However, these previously listed cell solutions:

• c8=3, h5=8, h4=2

have caused an interesing configuration to occur.

Possible locations left for candidate 9

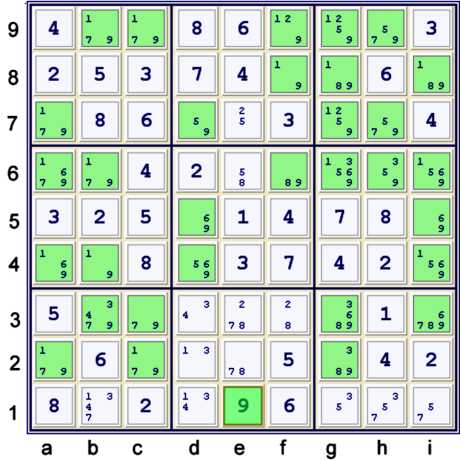
Although candidate 9 has many possible locations left on the puzzle grid, and only 1 bilocation strong inference set (9s in row 5), there exists a number of possible eliminations considering only candidate 9. All of these that I found share a consideration of the following two strong inference sets ( I call these sets simply strong sets here):

1. 9s in column h at h6, h79
2. 9s in row 8 at f8, gi8

The significant item to notice here is that gi8 and h79 share the same box. Hopefully, the elimination is now obvious.

Coloring with candidate 9 - a finned two string kite

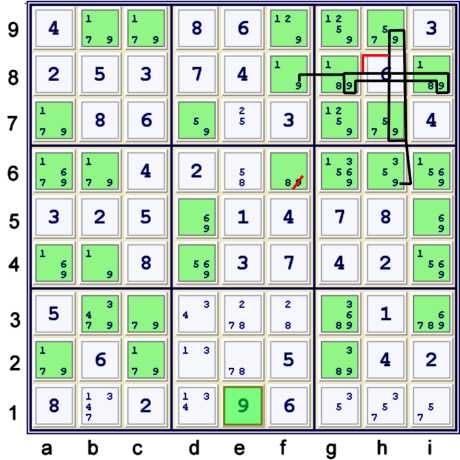
Because I am not an artist, the illustration of this elimination is not very well done. In fact, I find it harder to see after I have illustrated it than without the illustration. Hopefully, I can make this clear!

Poorly illustrated above is the following forbidding chain considering only candidate 9:

• f8=9 = gi8=9 -- h79=9 == h6=9 => f6≠9

A proof by contradiction is perhaps the easiest way to see that, no matter what, f6 cannot be 9.

• Suppose f6=9. Then both h6 and f8 cannot be 9.
• But, then both h79 and gi8 must contain 9. Since 9 cannot both be in row 8 and column h within box h8, as cell h8 is already assigned, we have an impossible situation!

After making this deductive elimination, the puzzle is reduced to a cascade of Unique Possibilities until all cells are solved.

Proof

1. Start at 23 filled - the given puzzle. Unique Possibilities to 26 filled. (UP 26).
2. Triple 134 at d123 forbids d7=1, d457&e23f3=3, d57&ef3=4 UP 27
3. Locked 8s at h56 forbids g6i56=8 UP 38
4. fc on 9s: f8 == gi8 -- h79 == h6 forbids f6=9 UP 81

• sets: 3 + 1 + 2 = 6
• Max depth 3 at step 2
• Rating: .07 + .01 + .03 = .11 (trivial)

Notes

Although this is a very easy puzzle, it is worth some study. Step 4 of my proof is a very easy coloring step, but nonetheless instructive. Using grouped arguments, such as the groupings used in that step, is not only very common, but also very powerful.

Coloring - or looking for eliminations involving only one candidate - is, in my opinion, a great place to start in understanding how chains work. The reason for this is three-fold:

1. Coloring eliminations are easy to consider, as one is only looking at one candidate
2. Coloring eliminations consider only strength in large containers (houses)
3. Almost ironically, things become complex and interesting faster with coloring - thus most of what one really needs to know about grouping of arguments is revealed through a study of coloring!

My last assertion, that most of what one really needs to know can be found just by studying coloring assumes that one views things in a general fashion. By that, I mean that one understands that thinking in groups is thinking in groups, no matter what form the group takes! Thus, if one understands an X wing, one understands a naked pair and a hidden pair. If one understands a swordfish, one immediately understands triples and naked triples. If one understands a depth 3 coloring elimination, one immediately understands all Y Wing Styles - including xyz wings, for example. The list can go on and on!

A didactic rant

A caveat: One should not limit their investigations into any technique, and especially coloring, to considering native sets that have only two possibilities left. The FACT that this will leave many eliminations unfound is easily illustrated by the concept of a swordfish, which considers three native sets limited to three possibilities each. If one wants to truly tackle logically the most difficult of sudokus, thinking in groups is absolutely required. For this reason, my definition of forbidding chains specifically starts considering Booleans. The Booleans can be used to represent any group that one finds to be useful! Once one accepts that simple concept, all techniques in sudoku become transparent.

Thinking in groups, or using groups, is done with all sudoku techniques. As such, it is not new. However, the most efficient way that I can fathom to fold all such thinking into a single concept is the use of Booleans within chains. Again, this is not new, nor is it different. Rather, it is merely a way to efficiently describe what everyone is doing regarding Sudoku solving! (Even those whom guess.)