A study in Chain Forging: Page 1

The following illustrated proof for the diabolical, extreme & almost unsolvable Tough puzzle of November 10, 2006 employs an imposing variety of techniques. Advanced Forbidding Chains, or Almost Alternating Inference Chains is my general description of the toughest ones used herein. As noted in the Unsolvable 16 solutions, any technique, may be used as an argument in the chain. If this is your first visit to this blog, WELCOME!!

The pace of new blog pages has screamed to a halt. Less frequent blog pages will be the rule from now on.

To Be or Not to Be

A point of interest here: The puzzle being tackled with this group of blog pages is The Reason that I decided to create this blog. The techniques that I used to solve this particular puzzle were the ones that I much wanted to convey to the rest of the sudoku solving world. Unfortunately, it has taken me a very long time to lay the foundation for a puzzle proof such as this one. I suppose that I grossly underestimated the depth, width and breadth of the foundation that I would require to solidly underpin this proof.

Since November 10 of last year, I have grown to have a deeper understanding of the derivations of many types of sudoku techniques. Specifically, I have learned that one basic trick essentially derives all Advanced Forbidding Chains, or Almost AIC type chains. This added learning caused me to revisit my previous proof of this puzzle. I found the puzzle much easier, and the proof that I will present on the following pages is much less deep. Finally, for me at least, this proof became much more visually apparent.

Certainly, the terminology used here is not the standard terminolgy used in many other Sudoku sites. Therefor, previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. Specifically, one may want to refer to the following pages:

• Locked Candidates
• Pairs, Triples, Quads
• Coloring
• Finding Coloring
• Y Wing Styles
• Finding Y Wing Styles
• Forbidding Chains 101 The Theory
• Forbidding Chains 102 The Practice How to Find 'em
• Advanced Forbidding Chains The theory of using techniques within Chains
• Almost Locked Sets
• Definitions: Most terms used on this page have a defintion somewhere on the defintions page.

The illustrations of forbidding chains, also called Alternating Inference Chains (AIC), shown in this proof will share this key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set(s)
• candidates crossed out in red = candidates proven false

Please be aware that, for me, strong and weak need not be mutually exclusive properties.

This puzzle is very difficult, thus the proof is very interesting. Please accept my gratitude for your forbearance!

Generally, I hope to show how to build upon previous knowledge to find complicated chains. For me, each technique learned is a building block for another technique.

The Puzzle as published

Hidden Pair 39, Hidden Pair 79, & Locked candidate 5

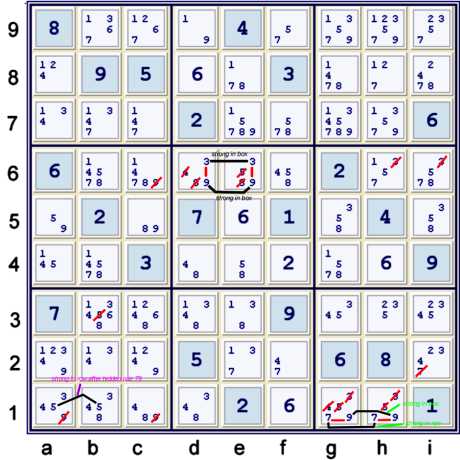
To save some space, I have chosen to illustrate a few steps simultaneously. Above, find:

• Hidden pair 39 at de6 => de6=39, c6≠9, hi6≠3
• Hidden pair 79 at gh1 => gh1=79, ac1≠9, i2≠7
• Locked 5s at ab1 => b3≠5

Some of these techniques are illustrated as wrap-around, or continuous, forbidding chains (AIC).

At this point, the puzzle is now very difficult. Normal techniques fail to make any advances. One absolutely needs something deeper.

Almost Y Wing Style using candidates 1 & 7

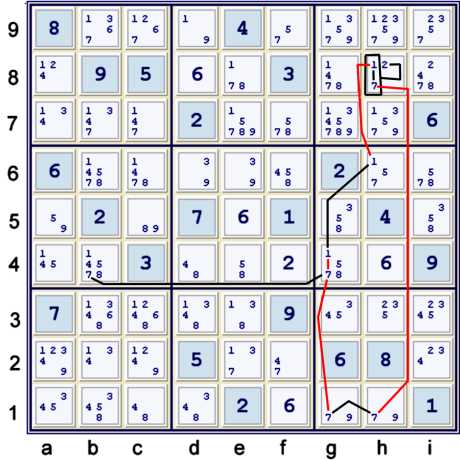
The little information that was garnered from the previous step, plus the original givens of both 1 & 7 in box e5 practically guarantee the existence of this almost relationship. Almost AIC are of no practical use by themselves, and need to be linked to a chain. In other words, their usefulness is for one of two equivalent reasons:

1. They establish derived strong relationships, such as h8=2 == b4=7 above
2. They establish derived weak relationsips, such as h8=17 -- g4=7 above

I prefer to view the relationships established as derived strong relationships, but there is no reason not to be aware of, nor not to use, the derived weak relationships.

Above, I have illustrated the Almost Y Wing Style 17:

• g4=1 == h6=1 -- h8=1 *==* h8=7 -- h1=7 == g1=7

This is an almost AIC chain, as cell h8 is not limited to only 17, but rather to candidates 127. I have also included above the strong relationship derived from the Almost Y Wing Style as:

• h8=2 ==₁ {g4=1 == h6=1 -- h8=1 ==₁ h8=7 -- h1=7 == g1=7} -- g4=7 == b4=7

Thus, I have established for the purposes of a larger chain:

• b4=7 == h8=2

Essentially, most of the markers for an almost chain like this are very simple:

1. g1=7 == h1=7
2. g4=1 == h6=1

Please note that from just the listed information, any cell in box h8 that contains both candidate 1 and candidate 7 is a potential {Almost Y Wing style using 17} cell.

Almost Y Wing Style using candidates 1 & 7 connected to a chain

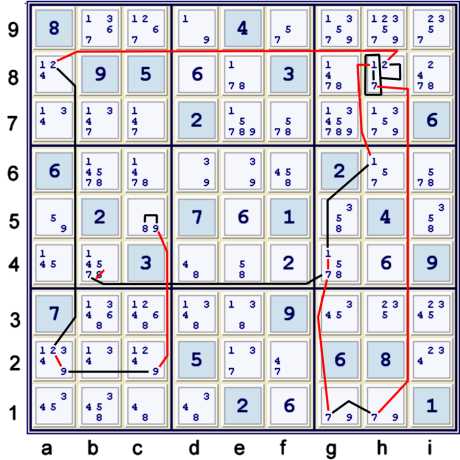
The illustrated step above takes the previously illustrated Y wing style and links it to a chain:

• c5=8 == c5=9 -- c2=9 == a2=9 -- a2=2 == a8=2 -- h8=2 == {Y Wing style 17:{h8=17,gh1=7, g4h6=1}} -- g4=7 == b4=7
• => b4 ≠8

This is much work to eliminate the lowly 8 from b4, but this is the nature of very tough puzzles. They are often gradually whittled down, and rarely solved in one big step. However, if one prefers just one big step, there is likely such a step possible. My preference is to keep each elimination step as short as possible.

Often, pieces of the same or similar information are used again. In this puzzle, the relationship between candidates 1 & 7 in boxes b5, h5 is a repeating key for me. Thus, the following step becomes easy to find given this last step.

Almost wrap around, or continuous, Y Wing Style using candidates 1 & 7

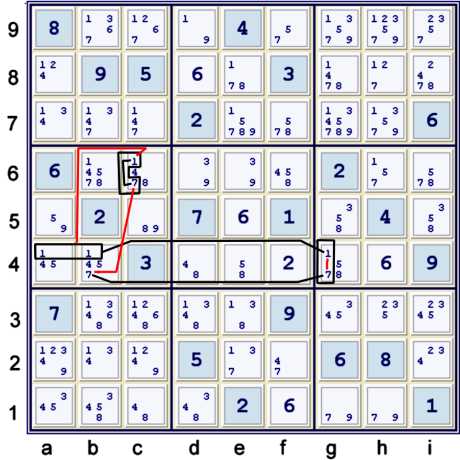
Previously, I have called a wrap around, or continuous, Y wing style my favorite type of chain. This type of chain is also a perfectly valid almost configuration. The example above is very similar to the previous example, with some interesting exceptions:

1. cell c6 contains 4 candidates versus h8, which contained only 3.
2. The strong relationship established is perhaps less transparent, until one practices with this type of deduction.

The almost chain illustrated above:

• c6=1 *==* c6=7 -- b4=7 == g4=7 -- g4=1 == ab4=1
is an almost wrap around chain. If the chain exists, then g4=7 == g4=1. Thus:
• c6=48 == wrap around Y style chain
• => c6=48 == g4=17

(c6=48 == something) is interesting, as the puzzle already contains a cell limited to 4,8. This cell, c1, happens to exist in column c. If one knows how to use Almost locked sets in a chain, the rest of the chain almost writes itself!

Almost Locked Set and Almost Y Wing Style chained together.

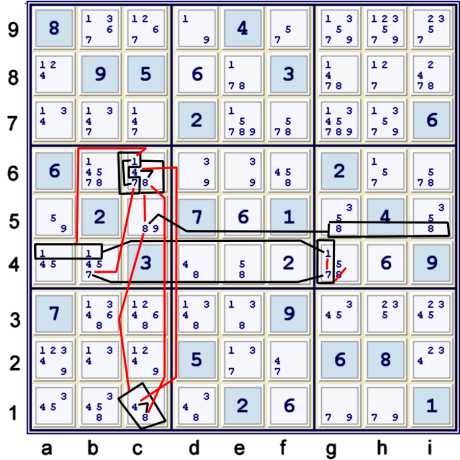
The graph of this step is much more complex than the step itself. Perhaps I need an education in art?! Let us break this graph down into managable pieces:

1. Almost wrap around Y Wing style 17 {bg4=7, abg4=1, c6=1748}
   • =>g4=17 == c6=48
2. Almost Almost Locked set 48 (c1=48, c6=4817}
   • =>{pair 48 at c16} == c6=17
3. c5=8 == gi5=8 in conjuction with 2
   • => gi5=8 == Y Wing Style 17 (bg4=7, abg4=1, c6=17}
   • => gi5=8 == g4=17 => g4≠8

Thus we have one chain that is really quite managable:

• {wrap around Y Wing style 17 {bg4=7, abg4=1, c6=17₁}} == {pair 48 at c16₁} -- c5=8 == gi5=8
• => g4=17 == gi5=8
  • => g4≠8

As a general idea, we have:

• Wrap around chain == wrap around chain -- single == Locked candidates

It is, in my opinion, the act of thinking in general ideas that makes finding such a chain less difficult.

For example, the concept of Almosting with Locked sets is often represented as a progression of almosting through degrees of freedom. I find this view helpful in writing proofs of generalized techniques, but I find it less than helpful in actually finding the chains on the puzzle grid. The key, often, is to view candidates in useful groups. The candidate groups are defined by the techniques they invoke (or, equivalenty, the techniques that invoke them!). Hopefully, this concept makes sense. It is vague, and that is because the translation into English of the very precise concept of Almost AIC is perhaps best left vague! I am fain to limit the possible types of interactions with more precise English. Mathematically, the concept is fully explained previously in this blog. All one needs is to allow the arguments in a chain to be Boolean variables, and one is finished with all the mathematics required!

Locked candidate 8

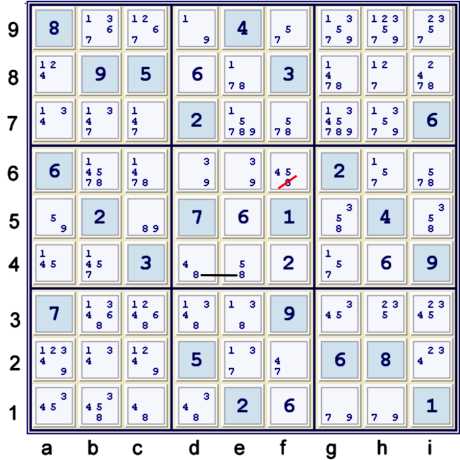
Now we have an easy step:

• d4=8 == e4=8 => f6≠8 => f7 = 8% column => 28 cells solved (UP 28)

The general theme of this page was Almost Y Wing Styles. Some other steps could have been taken first. I choose not to do this to illustrate as many interesting steps as possible. As this proof continues, perhaps think about how a different step order could make this solution significantly less lengthy.

This concludes the first page of this proof. There remain some very interesting steps. To find some of these, please visit the next page.