A study in Chain Forging: Page 8

Welcome back!

This proof page basically is more examples of using Almost single digit Coloring. Again, this concept has an alternate interpretation as appending a simple chain. The added complexity of appending a wrap around, or continuous chain is briefly investigated.

Previous pages of this proof are practically a prerequisite for this page:

1. First Page - Almost Y wing styles as Chain links
2. Second Page - Almost Hidden Pairs as Chain links
3. Third Page - Almost coloring, Almost AIC, Introduction to Appending chains
4. Fourth Page - An introduction to Super Cells
5. Fifth page - A further introduction to Appending Chains
6. Sixth page - Overlap of concepts: Super Cells as Appendages
7. page 7 - Almost Y wing Styles again, with appendages noted

Almost Coloring with 4s

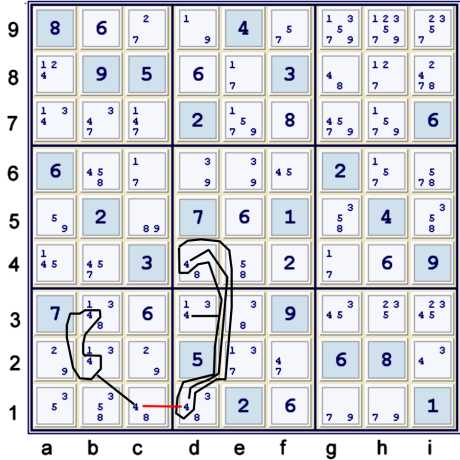
Above, I have illustrated the following almost chain on candidate 4:

• {fc on 4s: b23 == c1 -- d1 *==* d4}
• yielding the chain snippet or piece:
  • {fc on 4s: b23 == c1 -- d1 ==₁ d4} ==₁ d3=4

All that is needed is a relationship that leaves b4 and d4 strongly. What I mean is:

• The apparent focal point of the almost fc on 4's is b4 ≠4
• To complete the argument, one could use: b4=x == d4=y with {x,y}≠4

Almost Coloring with 4s chained

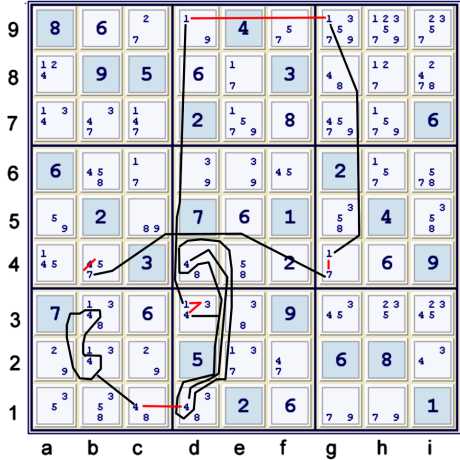
Above, one can use candidates 1 & 7 to accomplish the completed chain:

• {fc on 4s: b23 == c1 -- d1 ==₁ d4} ==₁ d3=4 -- d3=1 == d9=1 -- g9=1 == g4=1 -- g4=7 == b4=7
  • =>{b23=4 == d4=4} == b4=7 => b4≠4

Again, one can view this same chain as an appended bivalue/bilocation chain. Consider:

• d4=4 ==_{1 elimination appendage} {b23=4 == c1=4 -- d1=4 ==₁ d3=4 -- d3=1 == d9=1 -- g9=1 == g4=1 -- g4=7 == b4=7}
  • =>d4=4 == {b23=4 == b4=7} => b4≠4

The elimination appendage, d4=4, needs only the following two conditions:

1. it appends an existing strong set used in a potential bivalue/bilocation chain
   • Thus, here it appends d13=4
2. it sees the endpoint of the potential bivalue/bilocation chain
   • Thus, here d4=4 -- b4=4

I will attempt to quantify some of the types of appendages, and their prerequisites, in a follow-up blog. For now, consider that a conclusion appendage and an elimination appendage are similar. A conclusion appendage need not yield a chain that forbids any actual pencil marks.

The elimination, b4≠4, opens up another almost single candidate chain on 4s:

Almost Coloring with 4s again

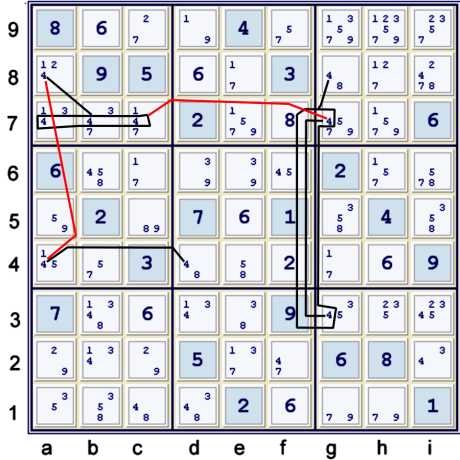
Another almost coloring chain on candidate 4 is illustrated:

• {d4 == a4 -- a8 == abc7 -- g7 *==* g3}
  • almost forbids d3=4, but for g8=4.

Again, one could look for: g8=x == d3=y with x,y≠4. Alternatively, one might look for g8=x == ??=4, where x≠4 and ?? sees d3. The chain illustrated below takes the latter of these two forms.

Almost Coloring with 4s chained again

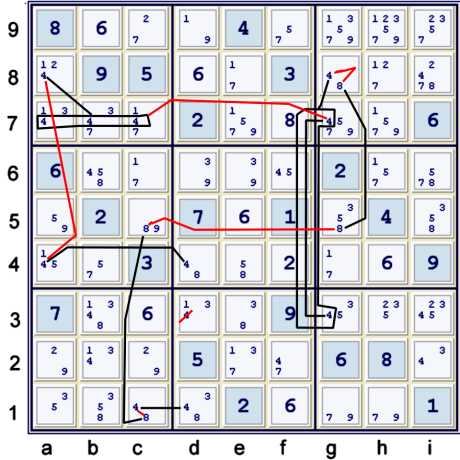
The complete chain above can be written as:

• {fc on 4s:d4 == a4 -- a8 == abc7 -- g7 ==₁ g3} ==₁ g8=4 -- g8=8 == g5=8 -- c5=8 == c1=8 -- c1=4 == d1=4
  • =>{d4=4 == g3=4} == d1=4 => d3≠4

One can alternatively view the possibility, g3=4, as an elimination appendage as follows:

• g3=4 ==_{1 elimination appendage} {d1=4 == c1=4 -- c1=8 == c5=8 -- g5=8 == g8=8 -- g8=4 ==₁ g7=4 -- abc7=4 == a8=4 -- a4=4 == d4=4}
  • => g3=4 =={d1=4 == d4=4} => d3≠4

Note that in this case, the elimination appendage, g3=4, appends a chain that but for g3=4 would be a wrap around, or continuous, chain. In this case, since the appendage is not in conflict with both the endpoints: {d1==d4} = 4, the resultant chain is not a wrap around chain.

Again, a more full theoretical treatment of appending chains will probably eventually occur in this blog.

After d3≠4, another almost coloring chain on 4s presents itself. Consider the newly stronger 4s in box e2. One may note, however, that essentially the same deduction is available without eliminating d3=4. Almost coloring on 4s is very prevelant in this grid.

Almost Coloring with 4s one more time

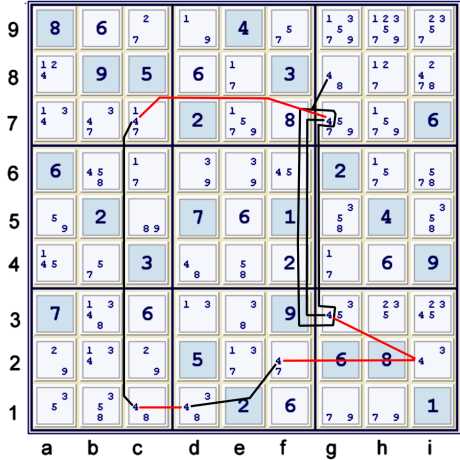
Above, but for the same 4 at g8, one has another almost coloring chain on candidate 4:

• f2 == d1 -- c1 == c7 -- g7 *==* g3
  • => i2≠4 == g8=4

Typically, one could look for another chain that emanates from g8 and also forbids i2=4. However, that is not the only possible type of chain to link with. One can also link with a wrap around chain. All one needs then is: g8=x == i2=4.

Almost Coloring with 4s chained into a wrap-around chain

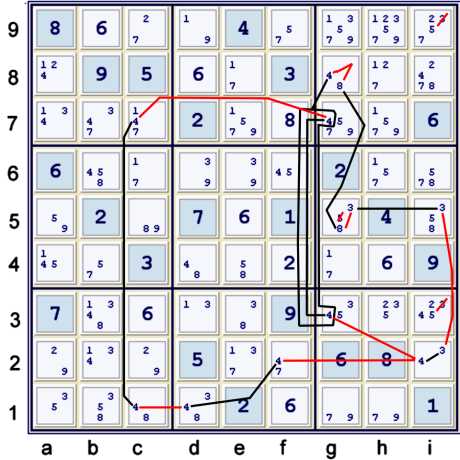
The chain above is rather interesting, as it forms what I have called, rather poorly, a partially discontinuous continuous loop:

• {fc on 4s: f2 == d1 -- c1 == c7 -- g7 ==₁ g3} ==₁ g8=4 -- g8=8 == g5=8 -- g5=3 == i5=3 -- i2=3 == i2=4
  • =>
    1. {f2=4 == g3=4} == i2=4, but since {f2=4 == g4=3} -- i2=4 we have wrap around thus
    2. g8=4 == g8=8 => nothing further, as we already had this
    3. g5=8 == g5=3 => g5≠5
    4. i5=3 == i2=3 => i39≠3

The advantage of the presentation of this chain in the fashion above is that it clearly demonstrates precisely which weak links are proven strong. The internal links of the almost fc on 4s are clearly not effected. However, in keeping with the idea of appending chains, there is also a simple chain appendage interpretation available:

• g3=4 ==_{1 weak strong intersection appendage} {g7=4 ==₁ g8=4 -- g8=8 == g5=8 -- g5=3 == i5=3 -- i2=3 == i2=4 -- f2=4 == d1=4 -- c1=4 == c7=4}
  • => ????

Here, a matrix analysis reveals clearly that g3=4 short circuits the wrap-around chain. However, the representation above does not clearly indicate this short circuit. It indicates the short circuit, just not clearly. At least it is not particularly clear to me. Again, I hope to better develop this series of ideas later. For now, be aware that the above is an appended chain. Also, be aware that appending wrap-around chains can require careful analysis. Hopefully, I will be up to the task of making everything more transparent. For this reason, I believe an understanding of the almost coloring concept is very important, as the almost coloring presentation of this elimination group leaves little room for deductive error.

Finally, after the eliminations noted above this puzzle becomes trivial!

Coloring with 5s

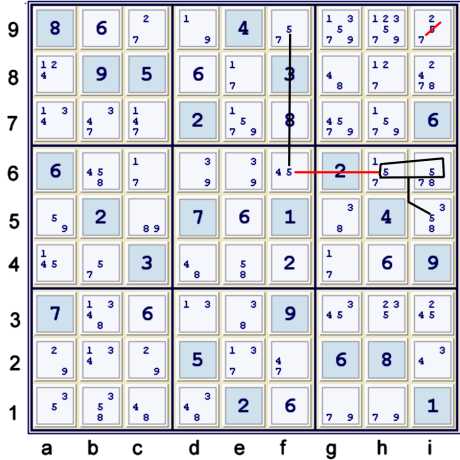
A short chain using only candidate 5 yields an easy elimination:

• i5 == hi6 -- f6 == f9 => i9≠5

After i9≠5, the naked pair 27 at ci9 unlocks the puzzle:

• i9=2 == i9=7 -- c9=7 == c9=2 => fgh9≠7 & h9≠2

All that is left is a cascade of Unique Possibilities to the end, starting with f9=5% cell.

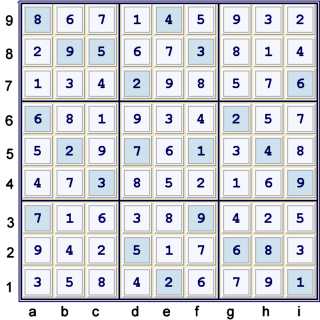
Solution

Notes

There are so many notes that I could write about this proof, that it is not easy to know where to start. I suppose that it may be best to allow one additional page. There I intend to publish a proof summary. Moreover, I intend to emphasize the common deductive threads introduced to tame this monster.