The following is an illustrated proof for the
Tough Sudoku of April 5, 2007. The main
techniques that I used to solve this puzzle are Y Wing Styles and
Coloring. By Coloring, I mean any technique that uses exactly one candidate to
justify an elimination.
You may wish to refer to previous blog pages to properly understand
this proof. Links to these pages are found to the right, under Sudoku Techniques.
This page illustrates only the deduced elimination steps that I choose to
solve the puzzle. Although many other steps are possible, they are not shown, as
to show every possible step is prohibitive in both time and space!
The information on the following blog pages may be helpful:
The illustrations of forbidding chains used in this proof will share the same key:
- black line = strong inference performed upon a set (strong link)
- red line = weak inference performed upon a set (weak link)
- black containers define a partioning of a strong set(s)
(not used)
- candidates crossed out in red = candidates proven false
Strong and weak need not be mutually exclusive properties.
Puzzle at start
A few Unique Possibilities are available here:
- b3 = 2% box & row (hidden single in both box & row)
- g4 = 3% box & column
- c6 = 7% box & column
Although there are many steps available at this point, such as the naked pair 12 at e46, the following
sequence of steps will render most of them superfluous.
Coloring with Candidate 3 (skyscraper)
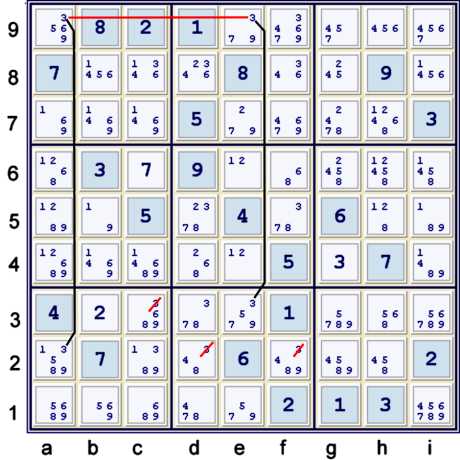
Above, the locations of the possible 3s conspire to make a very simple coloring elimination.
As a forbidding chain on 3s:
- a2 == a9 -- e9 == e3 => c3,df2≠3
As a proof by contradiction:
- Any of c3,df2=3 => a2 & e3≠3 => a9 = e9 = 3,(singletons in columns), thus too many 3s in row 9
These eliminations do not directly solve any cells, but they are a set up for a short sequence of
steps.
Hidden Pair 13
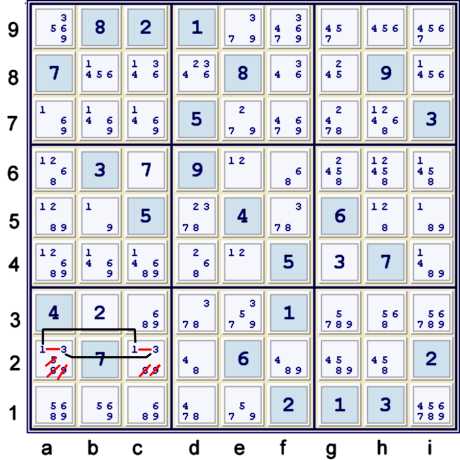
Since both candidates 1 & 3 are limited to the same two locations, a2,c2, in a house(s), no other candidates can exist in those two cells. I have illustrated the elimination
as a short continuous nice loop forbidding chain, or Alternating Inference Chain (AIC).
One could alternatively use the naked quad 5689 at abc1,c3 to make the same eliminations. Also,
if one does use the naked quad, then one can also make the next eliminations at the same time.
Locked candidate 5
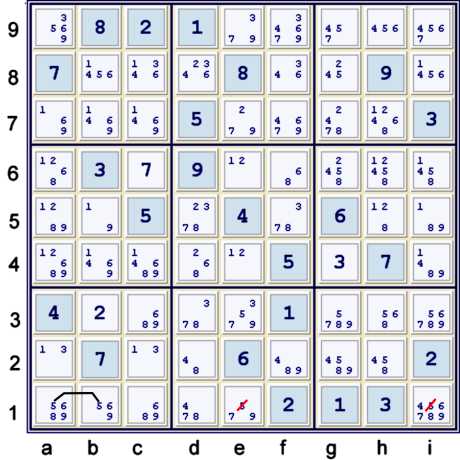
Illustrated above, the 5s in box b2 are limited to two locations, ab1. Since both of these
locations exist in row 1, 5 cannot exist in row 1 outside of box b2.
If one had used the naked quad instead of the hidden pair 13, one could have made the elimination
of these two 5s at the same time, as the naked quad locks the 5s into the same cells.
After eliminating the 5s from ei1, a cascade of Unique Possibilities (hidden and naked singles)
occurs until 53 cells are solved. The cascade begins with e3 = 5% box & column, which then allows one
to solve all the 3s on the puzzle grid. The cascade continues until one gets to the next illustration.
Again, a handful of easy steps are possible below. However, either one of the next steps illustrated, or
something equivalent to one of them, is all that is required to unlock the puzzle.
Y Wing Style using candidates 4 & 5
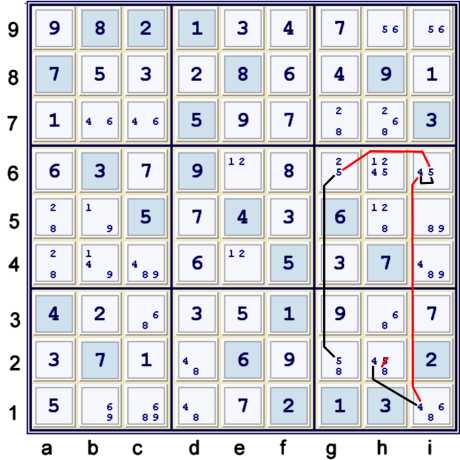
The Y wing Style illustrated above uses the cell i6=45 as the vertex:
- i6=4 => i1≠4 => h2=4 => h2≠5
- i6=5 => g6≠5 => g2=5 => h2≠5
As a forbidding chain, the step can be written:
- h2=4 == i1=4 -- i6=4 == i6=5 -- g6=5 == g2=5 => h2≠5
As a strong inference set list, the step is also detailed:
- g26=5, i6=54, i1h2=4 => h2≠5
In a strong inference set list, each set listed must meet only this requirement:
- At least one of the items in the set must be true
Since the forbidding, or weak, links are universal, there is usually no need to detail them.
Alternate to the previous step - Y Wing using candidates 568
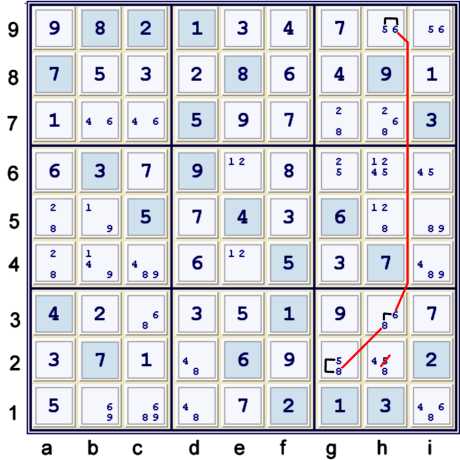
Illustrated above, a standard Y Wing (also a subset of Y Wing Styles), justifies the same
elimination. The Y wing considers cell h3=68 as the vertex:
- h3=6 => h9≠6 => h9=5 => h2≠5
- h3=8 => g2≠8 => g2=5 => h2≠5
As a forbidding chain, one could write:
- g2=5 == g2=8 -- h3=8 == h3=6 -- h9=6 == h9=5 => h2≠5
As a strong inference set list:
- g2=58, h3=86, h9=65 => h2≠5
No matter how one finds it, once 5 is forbidden from h2, the puzzle is reduced to a cascade
of Unique Possibilities until all cells are solved. (UP 81).
Proof
- Start at 23 filled - the given puzzle. Unique Possibilities to 26 filled. (UP 26)
- fc on 3s: a2 == a9 -- e9 == e3 forbids c3,df2=3
- Hidden pair 13 at ac2 forbids a2=589, c2=89
- Locked 5s at ab1 forbids ei1=5 UP 53
- Y wing style: g2=5 == g6=5 -- i6=5 == i6=4 -- i1=4 == h2=4 forbids h2=5 UP 81
- Sets: 2 + 2 + 1 + 3 = 8
- Max depth 3 at step 3
- Rating: 2(.03) + .01 + .07 = .14 (perhaps a bit easy for the tough label)
Notes
This puzzle is an excellent puzzle for study for someone who wants to tackle the tougher puzzles.
It is not too difficult, but it does at least require some advanced steps.
Hopefully, the illustration of the last step as either a Y Wing Style or a standard Y Wing
is a sufficient demonstration of the fact that both steps are completely equivalent in complexity.
The logic for each is precisely the same. Only the nature of the strong inferences is slightly
different. Personally, I find the Y Wing Style using only two candidates, 4 & 5, to be slightly
easier than the standard Y wing using 3 candidates. No matter which one finds easier though, it
is useful to have both in one's bag of tricks.