Proof of Tough Sudoku January 14, 2008

The following illustrated proof for the Tough Sudoku of January 14, 2008 employs a small group of Sudoku techniques, tips and tricks: Hidden Pairs, Almost Y Wing Style, Locked Candidates, and Alternating Inference Chains.

Previous blog pages may be helpful. Links to these pages are found to the right, under Sudoku Techniques. This list is getting long, so specifically, one may want to refer to the following previous blog pages:

• Locked Candidates
• Pairs, Triples, Quads
• Y Wing Styles
• Finding Y Wing Styles
• Forbidding Chains 101 The Theory
• Definitions: Most terms used on this page have a defintion somewhere on the defintions page - although an update is long overdue.

Many steps not illustrated are possible. To show every possible step is, well, just overkill. However, this page illustrates sufficient deduced elimination steps to both solve the puzzle, and also to prove a unique solution.

The illustrations of forbidding chains, also called Alternating Inference Chains (AIC), shown below will share this key:

• black line = strong inference performed upon a set (strong link)
• red line = weak inference performed upon a set (weak link)
• black containers define a partioning of a strong set(s)
• candidates crossed out in red = candidates proven false

Please be aware that, for me, strong and weak need not be mutually exclusive properties.

Style Change

Previously, I had abandoned using the chessboard algebraic notation in favor of the more common rc notation. However, since many people have begun again to post proofs on the tough pages, I am hereby returning to algebraic notation. I will retain some of the Eureka-like qualities of writing AICs, though. Hopefully, this does not create too much confusion for those from either group. Illustrations will include the cell descriptive labels to help with interpretation.

The Puzzle

Typically, at this point, and more so if I am solving the puzzle on paper, I prefer to search for Hidden Pairs before filling in the Possibility Matrix. There is 1 hidden pair immediately available based upon the givens.

Step 2 - Hidden Pair 15

Steps 3abc - Locked Candidates 8, 8, & 4

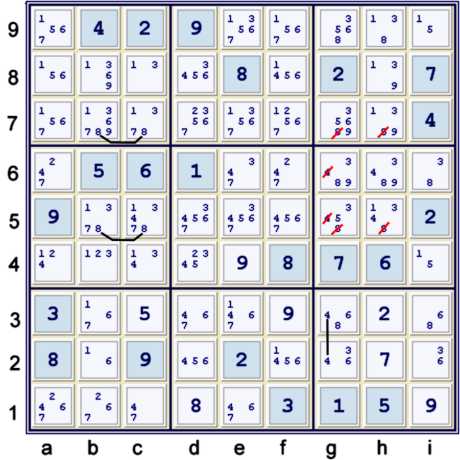
Above, the following three steps are taken:

• 3a Locked 8's bc7 => gh7≠8
• 3b Locked 8's bc5 => gh5≠8
• 3c Locked 4's g23 => g56≠4

An AUR digression

Although I do not use this step, steps 3a, 3b make it hard to avoid seeing

• (7)a6=(Hidden Pair 78)bc5-by AUR(Hidden Pair 78 bc7)=(7)a79
• => a1≠7
• => mental note, exactly one Hidden Pair 78 will exist at bc5, bc7

The logic: By AUR (Almost Unique Rectangle) we cannot have Hidden Pair 78 at both bc5 and bc7. Since there are no 7's possible at bc4689, (7) must exist in column a in at least one of boxes b5, b8. Of course, one can also make the same deduction using:

• (7)b13=(Hidden Pair 78)b57-by AUR(Hidden Pair 78)c57=(7)c1
• =>a1≠7

In my opinion, Almost Hidden Pair generated AUR deductions are more prevalent than Almost Naked Pair generated AUR deductions.

Sudoku Strategy: Puzzle Mark UP

Before marking up the puzzle, I also took the following steps that are not required:

• Locked 1s b23 => b4578≠1
• Locked 4s ac1 => e1≠4
• Locked 6s g79 => g23≠6

I print out the current Possibility Matrix and mark the grid. My mark ups have evolved over time. Currently, I circle all the endpoints of bilocations sis - meaning I circle a candidate each time it has only one other location in a box, column, row. I also underline a candidate if within a row or column it has only one location in one box, but multiple locations in exacly one other box. Finally, I mark with a pointed v any deductions that I see immediately available if the underlined candidate conjugates are true.

In the mark up below, I aborted the mark up once I marked candidates 1, 2, & 3. There seemed little reason to continue!

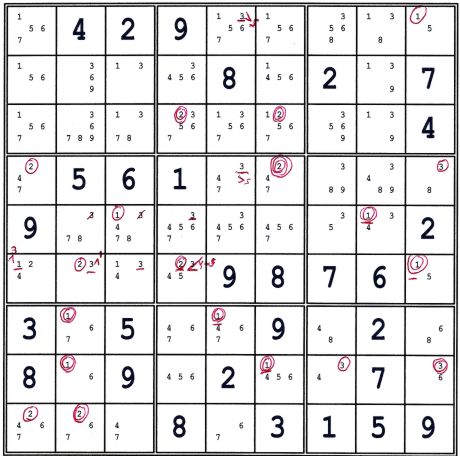
Above, once I started to mark-up candidate 3, I noted and marked:

• (3)e6=(3)ghi6-(3=5)g5
  • Thus (3)e6 is underlined with a pointing v5 towards g5
  • I could not miss the continuation: -(5)i4=(5)d4
  • => I found a Y Wing Style35 => d4≠3
  • Thus the (3) at d4 is also crossed out.
• (3)e9=(3)gh9, thus (3)e9 is underlined. However, an almost Y wing style struck me:
  • [(3)g9=(3-8)h9=(8)h6-(8=3)i6] -(3=5)g5
  • => (3)e9=(5)g5
  • Thus, I also placed v5 by (3)e9 pointing at g5.
• Since (3)e6-(3)e9, and since both are marked with the same strong inference: =(5)g5,
  • (5)g5 was a certainty.
  • (5)g5 seemed likely to advance the puzzle quite far, and the deduction was only depth 4
• 'Twas time to stop and record the advances

The idea of the mark-up that I use is to bring to fore hidden strengths. Thus, circled candidates are noted, but generally not v'd because this would over populate the grid. The Possibility Matrix is already biased to expose Naked strengths (cells). The most difficult essentially bivalue strengths to find for me are those derived from the underlined candidates. Thus, if they seem to be easily linked, they get the v's. However, if the mark-up starts to get too populated with marks, I generally retain the v's, but make notes instead of marking the possibility matrix. Thus, for this puzzle, my notes would have already included a1≠7 by AUR. Note also that the mark-up was updated not only with d4≠3 but also with the immediate locked candidate deduction that followed, and the stronger 3's in columns bcd underlined at d5, bc4.

There are many ways to get hidden information out of the Possibility Matrix. I believe one should toy with which manner works well for the individual. Oftentimes, I change my mark-up technique slightly to suit the particular puzzle.

Step 3d - Basically a partially hidden xyz chain

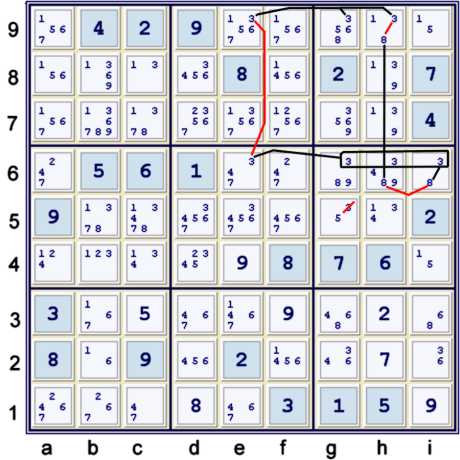
The elimination graphed above has many interpretations possible. The way I found it would be written:

• (3)ghi6=(3)e6-(3*)e9=[(3)g9=*(3-8)h9=(8)h6-(8=3)i6 =>
  • (3)ghi6=[(3)g9=(3)i6] => g5≠3
• However, one may prefer:
• (3=8)i6-(8)h6=(8-3*)h9=[Finned X wing candidate 3: g9=*e9-e6=ghi6]
  • => g5≠3
  • This latter representation is more likely to be found if one is counting, or actively looking for almost coloring steps.

Probably, the latter representation is more acceptable to some, as it uses well-defined AIC fragments. However, the Almost Y Wing Style is a favorite fragment of mine. If one uses counting, then no knowledge of any fragments is required - but - I think fragment recognition speeds the process tremendously.

After making the elimination, (5)g5 % cell causes a cascade of hidden and then naked singles to the end.

Solution

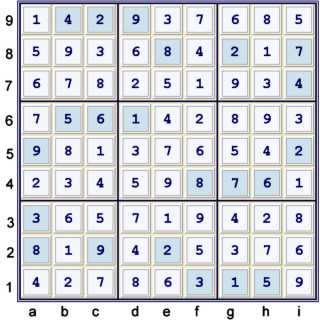
Notes

Puzzle spectrum:

• Sets: (3)1+(2)+(4) = 9
• Max depth 4 at step 3d.
• Rating: (3).01 + .03 + .15 = .21 - certainly not worthy of SE 8.3 rating!

Probably, this is one of those puzzles that just happened to have the type of chain available that is easy for me to stumble upon.

This puzzle may be about right for a tough. It cannot be solved without resorting to something beyond the standard pairs, triples, locked candidates. As is often the case, the awareness of Y wing Styles, and techniques much like them, quickly keys the solution.