The
Tough Sudoku of August 16, 2009 contains another excellent example of the power of using Quantums,
although it is a very simple form of quantum set. Once again, a MUG, or Multi-value Universal Grave, is utilyzed. One could delay
the use of the MUG, and simply employ a Uniqueness loop instead. However, I decided to demonstrate
that one need not wait. For kicks, I have included a solution which does not use uniqueness somewhere at the bottom of the page.
A MUG is an advanced sudoku solving strategy, tip or trick. However, MUGs can be both trivial to locate and employ.
It seems that whatever manner in which Gath finds puzzles utilyze patterns which, at least recently, are likely to produce MUGs. Thus, these
animals may be of particular usefullness. On the other hand, one can go a long time without finding a useful one in a puzzle.
If this is your first visit to this blog, welcome! Unfortunately, if you are a first time visitor, this page may seem
like it is written in a different language. Well, it is!! Previous blog pages may be helpful. Links to these pages are
found to the right, under Sudoku Techniques. The earliest posts are at the bottom, and if you have never perused
the intricacies of our special coded language here, you may wish to start close to beginning. The list is rather large, so below
find a list of links that may be pertinent to this particular puzzle.
The Puzzle
Three UPs are available here.
A Lowly Naked pair
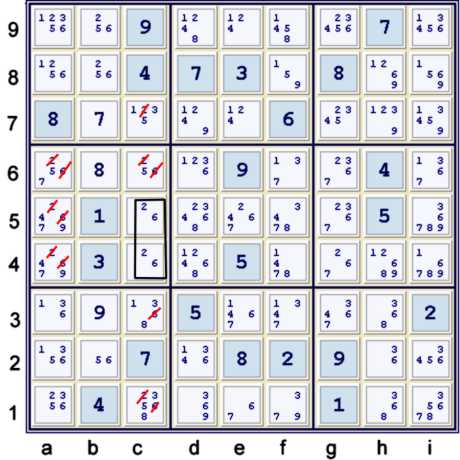
Naked pair (26) c45 advances the puzzle to UP 33. It shall perform again, however.
A generally hidden, often permeable, MUG
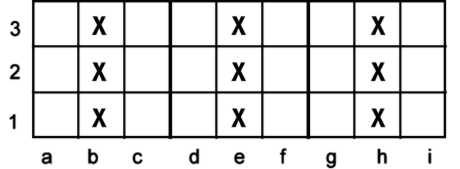
Above, the X's are meant to demonstrate a swordfish pattern contained in exactly three
boxes. Two swordfish patterns (meaning using two candidates) using exactly the same cells, contained in exactly three boxes,
exactly three columns, and exactly three rows, cannot exist in a Sudoku that has a unique solution. Important to
most such patterns is that none of the candidates forming the swordfish pattern can be Givens. It is not important that
the pattern be full, however. For example, b1, e2, and h3 could be proved devoid of one or
both of the candidates and the pattern would still hold. Of course, in that case, it would default
to a simple Uniqueness Loop of pairs. In fact, one can use that Uniqueness Loop to derive this MUG.
Here is one simple derivation: For the purpose of this derviation, suppose that swordfish using
candidates (1) & (2) exist at b123, e123, h123.
- at b123, exactly one of b123 is not (12). Because of the symmetry of this pattern,
we can clearly arbitrarily suppose that b1 does not contain (12).
- In similar fashion, we can arbitrarily suppose that e2 does not contain (12)
- Again, we can arbitrarily suppose that h3 does not contain (12)
- We are left with (pair12) at b23, e13, h12.
- We are also left with (Pair12) at be3, he1, bh2.
- One may recognize this as a Unique Loop, if not:
- Since we have (pair12) in each of three boxes, b2, e2, h2
- And in each of three columns: beh
- And in each of three rows: 123
- Nothing can occur outside of of these six cells to uniquely determine their values
- Thus, only something internal to at least one of the cells could determine the
value of these six cells.
- There exists no information available to make this determination
- The puzzle cannot be resolved uniquely
That is a rather long-winded argument. Please forbear that!
IMO, one can derive all MUGs, including this one, without needing to resort to case by case investigation.
One can, imo, show that overlapping loops negate the resolution power of the sis that could be
used to resolve the sis. Every continuous loop/net inhibits the resolution power of each
sis considered. Although there exists, within sudoku, plenty of resolution power,
extreme overlap can cause a lack of information such that it is impossible to reduce the possibilities in each sis to 1.
In any event, perhaps it is time to return to the puzzle
A Lowly Naked pair, A Lowly Naked Triple, and therefor a MUG
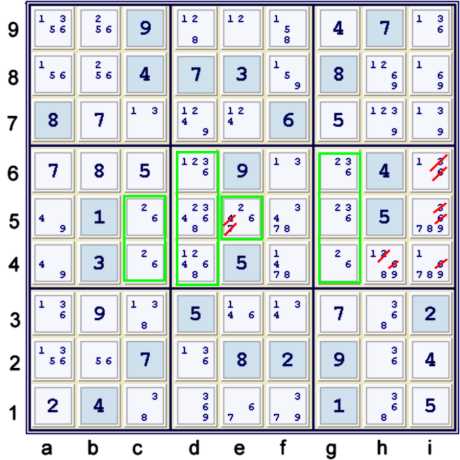
Naked pair (26)c45 was previously noted. Newly existent Naked Triple(236) at g456 makes some
more eliminations, noted in box h5. However, both of these items together means that (26) is limited to
c456 and g456. Therefor, using the MUG noted, (26) cannot be limited to d456. There exists exacly
one location within box e5 for (26) outside of d456. Either (2) or (6) must reside at that location,
e5. Hence, using the MUG one can write the following very long and complex quantum chain:
Given that the derivation of the MUG uses (NT236)g456, one may as well make those eliminations at the
same time. The puzzle is reduced to singles.
Mugged Solution Path
- Start 22 UP 25
- (NP26)c45 => a456,c1367≠26, UP 33
- (NT236)g456, (NP26)c45, MUG(26)cdg456 => (2=6)e5 =>
- e5≠47, h4.i456≠236, UP 81
Alternate path, no uniqueness assumption required
- Start 22 UP 25
- (NP26)c45 => a456,c1367≠26, UP 33
- (HP78)i45 => i45≠1369, UP 39
- (3=9)i7 - d7 = (9-3)d1 = (3-1)d2 = a2 - c3 = (1)c7 => c7≠3, UP 81
For those who wish to read further on MUGs, I suggest the following two forum topics:
Discussion about MUGs.
Discussion about permeable and impermeable MUGs