The following is an illustrated proof for the
Tough Sudoku of February 15, 2007.
This tough puzzle is well suited for the study of the limited
techniques required:
- Locked candidate
- Hidden Pairs
- Coloring
- Y Wing Style
You may wish to refer to previous blog pages, although it probably is not required. Links to
these pages are found to the right, under
Sudoku Techniques.
It is not the goal of this page to show every possible step.
By Coloring, I mean a forbidding
chain on just one candidate. If one studies coloring, one can learn just about everything one
really needs to know in order to perform forbidding chains on more than one type of candidate.
Forbidding chains on just one type of candidate can get very complex. The examples today are very
simple.
By Ywing style, I mean a forbidding chain that is logically analagous to a Ywing.
Some defintions
The following terms are employed in the explanations below:
- %
- is a singleton in
- strong set
- A set such that at least one of its members must be true
- weak set
- A set such that at most one if its members can be true
- If A & B are members of a weak set:
- A = true implies B = false
- B = true implies A = false
- native
- Naturally occurring in the current puzzle possibility matrix without
making any deductions
- House
- A cell, box, column, row
- Unique Possibilites
- A cell that is solved because it is uniquely defined in a house.
- UP
- Acronym for Unique Possibilities
- =>
- implies
Please note that a weak and strong need not be mutually exlusive properties. In other words,
a set that is strong may also be weak. More precise definitions are available on the
Definitions page of the blog.
Puzzle at start
A few Unique Possibilities:
- b3 = 3% box & row
- b2 = 4% box
- g3 = 4% box & row
- i3 = 6% box and row
b3 = 3% box & row means b3=3 because it is the only possible place for 3 in box b2 and
also in row 3. Of course, one need only find one of these two restrictions to place the 3.
Puzzle at UP 27
Hidden Pair 69
Hidden pairs are easily found if one notices a symmetrical alignment of two candidates relative
to a house. At the left, 6,9 at cells f1,f3 (f13 for short) and d79 limit both 6 & 9 to two cells
in box e5. If something other than 69 were to go into those two cells, there would no longer
be enough places for either 6 or 9 in box e5.
Locked Candidates with 1s
Illustrated to the left, the 1 at c1 limits 1s in box h2 to ghi2. If e2=1, then there would
be no places left for 1 in box e2. Thus, e2≠1. Since we already know e46 cannot contain
1, we now have e3 = 1% column.
Hidden Pair 23
A hidden pair 23 is revealed at h78 considering the 23's in column g and row 9 interacting
with box h8. In this case, one can also now use the locked candidates property of both 2 & 3 at
h78 to remove 3 from h45 and 2 from h12.
coloring on 7s
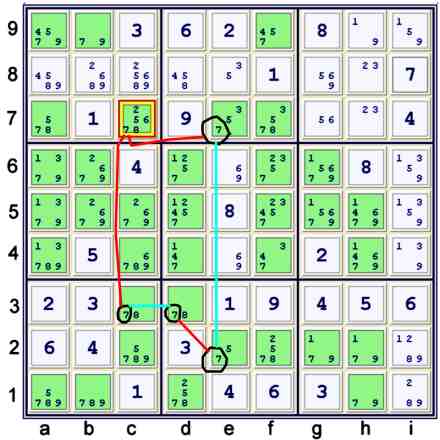
Above, the possibility matrix is now considered. All the current possible locations for 7
are highlit green. The following key is used here and in the next few steps:
- black circles = members of strong sets
- blue lines = indicate in which house the strong sets reside
- red lines = indicate a forbidding or weak link
- endpoints of the red lines are members of a weak set, or weak subset
- If two red lines point at a candidate, that candidate is eliminated.
The elimination above is also called a
two string kite. The logic for the elimination
can be expressed in many ways. Here is one way:
If c3=7, then c7≠7
If c3≠7 then considering the possible 7's in row 3, d3=7
If d3=7, then e2≠7
If e2≠7 then considering the possible 7's in column e, e7=7
If e7=7 then c7≠7
Conclude: Whether c3=7 or c3≠7: c7≠7
In every case where such an elimination is justified, if one supposes that the eliminated
candidate is true, then a contradiction will exist somewhere within the strong and weak sets
considered - using only those strong and weak sets. In fact, depending on where one starts,
one can prove a contradiction in any weak and strong set considered. For example,
suppose c7=7:
- c7=7 => e7≠7 => e2=7 => d3≠7 => c3=7, but: 2 7's in column c.
- c7=7 => c3≠7 => d3=7 => e2≠7 => e7=7, but: 2 7's in row 7
- c7=7 => (c3≠7 and e7≠7) => (d3=7 and e2=7), but: 2 7's in box e2
All of these relationships, and the elimination, are succintly contained in the forbidding chain:
- fc on 7's: c3=7 == d3=7 -- e2=7 == e7=7 forbids c7=7
Please refer to a previous blog page if you want to understand forbidding chains.
coloring on 8s
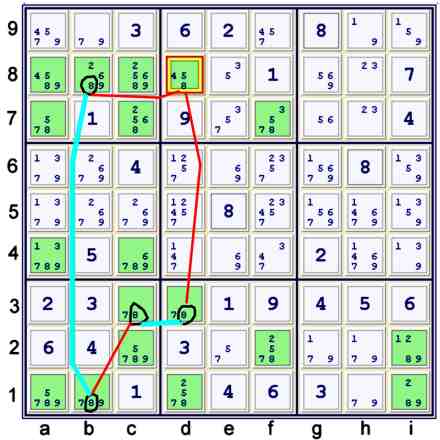
Illustrated above is another two string kite, this time considering candidate 8.
One can start the illustrated idea from any circled point above, or from d8=8 (which will then
be proven false). Again, the real clue to finding such an elimination are the strong sets
considered:
- c3=8 OR c4=8
- b1=8 OR b8=8
Written as a forbidding chain:
- d3=8 == c3=8 -- b1=8 == b8=8 forbids d8=8
Clearly, after d8≠8, f7 = 8 %box.
Finding the Y wing style pattern
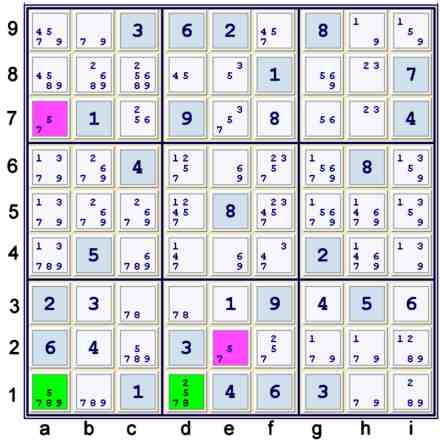
Illustrated above is all the information that one must notice to find a Y wing style pattern.
I call the pattern found above very common, as it is very common. One needs
to recognize:
- e2=57 (cell e2 is limited to 5 OR 7)
- a7=57 (cell a7 is limited to 5 OR 7)
- ad1=5 (Fives in row 1 are limited to cells a1,d1)
- a1 shares a house with a7 (column a)
- d1 shares a house with e2 (box e2)
Graphical illustration of the Y wing style
Illustrated to the left is the justification for removing 7 from e7. Again, there are many
ways to interpret the relationships graphed. Here is one way:
- a1=5 => a7≠5 => a7=7 => e7≠7
- a1≠5 => c2=5 => e2≠5 => e2=7 => e7≠7
- clearly, e7≠7
As a forbidding chain:
- a7=7 == a7=5 -- a1=5 == c2=5 -- e2=5 == e2=7 forbids e7=7
Although the first representation may at first seem more clear to you, the forbidding chain
representation, in my opinion, is better as it completely details why, for example,
a1≠5 => c2=5. The reason being: {a1=5, c2=5} are a strong set.
After eliminating the 7 from e7, the puzzle is solved using only Unique Possibilities. Most
of these are %cell, but there a a few hidden singles one must find - such as e2=7% column and
a7=7% row.
Solved Puzzle
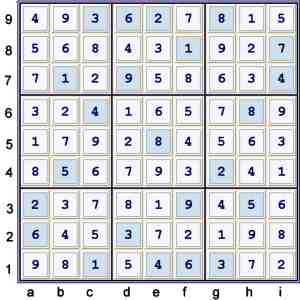
Proof
The following proof uses some, but not all of the steps detailed above. It also uses a step
not detailed. Instead, this proof represents the lowest rated solution that I found.
- Start at 23 filled - the given puzzle. Unique Possibilities to 27 filled. (UP 27).
- Locked 1's at de3 forbids e2=1
- fc on 8's: d3 == c3 -- b1 == b8 forbids d8=8 UP 29
- e2=7 == e2=5 -- c2=5 == a1=5 -- a7=5 == a7=7 forbids e7=7 UP 36
- Locked 5's at e78 forbids e26=5 UP 81
- sets: 1 + 2 + 3 + 1 = 7
- max step depth: 3 at step 3
- Rating: .01 + .03 + .07 + .01 = .12
ICY

Perfect weather for Valentine's Day!