Steps to Solve Tough Sudoku of 24-Jan-2007 with Proof

The following is an illustrated proof for the Tough Sudoku of 01/24/07. Since this proof uses forbidding chains, you may need to refer to previous blog pages to understand this proof. Links to these pages, including Forbidding Chains 101, The Theory, are found to the right, under Sudoku Techniques.

Puzzle at start

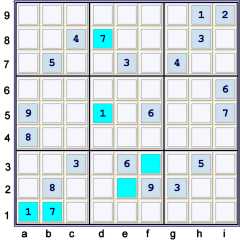A few Unique Possibilities:

• i4 = 3% box & column
• b5 = 3% row
• a9 = 3% row, box & column
• i8 = 5% column

Now at UP 26, (or at the start), note also Hidden pair 17 at e2f3. Thus e2f3 are limited to only 17.

Possibility Matrix at 26 filled

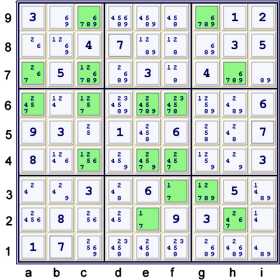In column i, both 1s and 4s are locked in box h2. Forbids:

• h12 = 4
• g3 = 1

3 strong sets with the 7's:

1. a67 = 7
2. h72 = 7
3. gf3 = 7

Beg this forbidding chain on 7's:

• a6 == a7 -- h7 == h2 -- g3 == f3 forbids f6=7

Yielding this new possibility matrix:

Possibility Matrix again at 26 filled

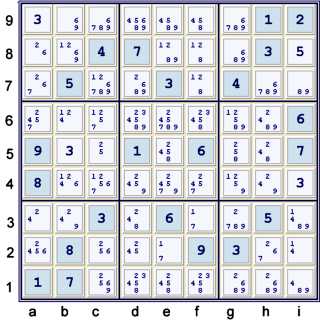
Most normal techniques fail to advance this puzzle further. In order to properly analyze this puzzle at this point, I print it out and mark it up. Often times, the act of marking the puzzle makes a few forbidding chains obvious.

Puzzle Mark-up at 26 cells solved

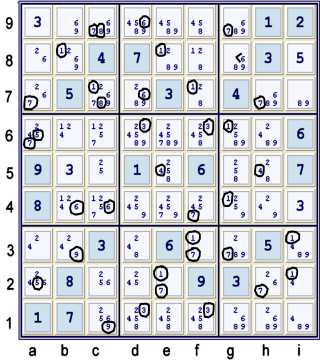
Refer to the page, Forbidding Chains 102 The Practice for an in depth explanation of my puzzle markings at this stage. I have added the black V at g8 because of the 26 at a8 and 69 at b9.

Of special interest are the endpoints of strong links in the following cells: a6, c7, c9. Two of these three beg the following:

Depth 4 Forbidding Chain

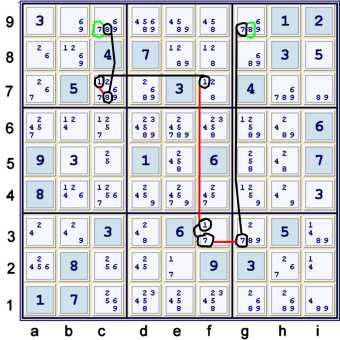Key:

• Black circles = endpoints of strong links
• Black lines = strong links
• Red lines = weak links
• Green circles = elimination targets

This forbidding chain is an excellent example of mixing the use of strength in location and strength in cells. It can be written as follows:

• c9=8 == c7=8 -- c7=1 == f7=1 -- f3=1 == f3=7 -- g3=7 == g9=7
  • forbids c9=7 and
  • forbids g9=8

One can now solve the following cells:

• g9 = 7% row
• h2 = 7% box & column
• f3 = 7% box & row
• e2 = 1% cell
• i3 = 1% box, row, & column
• i2 = 4% cell

Yielding Unique Possibilities to 32 cells filled (UP 32).

                       New Possibility Matrix at UP 32

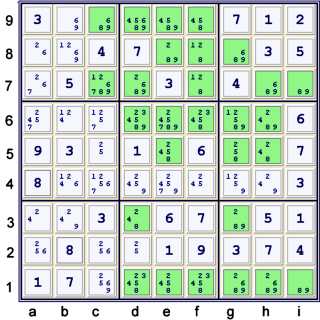Here we have the following Locked candidate eliminations:

• Locked 4's at ab3
  • forbids d3=4
• Locked 6's at ac2
  • forbids c1=6

There are a few forbidding chains on 8's possible. One that gets all the eliminations in one step is commonly called a finned X wing. Note these strong sets:

1. d3, g3 = 8
2. g8, ef8 = 8

Thus the following forbidding chain on 8's:

• d3 == g3 -- g8 == ef8 forbids d79=8

Once again, most normal techniques fail to advance this puzzle further. One could do another puzzle mark-up, but not that many changes have occurred. I often just use my old mark-up at this point. Happily, the possibly pivotal 6 at g8 yields some eliminations.

                       Y wing style elimination #1

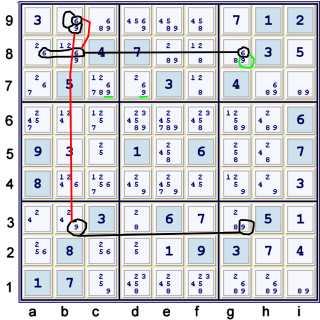Key as as before.

The following strong sets are considered:

1. g8, ab8 = 6
2. b9 = 6, 9
3. b3, g3 = 9

The strong link:

• g8=6 == ab8=6

is a common trick.

b9 = 69 is the vertex of the Y.

Forbidding chain representation of this step:

• g8=6 == ab8=6 -- b9=6 == b9=9 -- b3=9 == g3=9 forbids g8=9

After this step, we have the additional eliminations:

• Locked 9's at hi7 forbids cd7=9

Y wing style eliminations #2

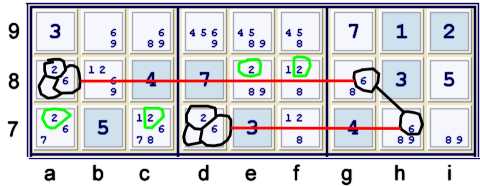
This elimination type I find to be very common. The 6's at g8h7 form the vertex of this Y. Here is this step as a forbidding chain:

• a8=2 == a8=6 -- g8=6 == h7=6 -- d7=6 == d6=2
  • forbids ac7,ef8 = 2

Y wing style elimination #3

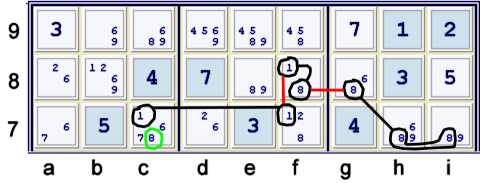
Here, f8=18 is the vertex. Notice again that a candidate is grouped within a strong set. In this case, the 8's in box h8 are grouped according to rows. Here is this step as a forbidding chain:

• c7=1 == f7=1 -- f8=1 == f8=8 -- g8=8 == hi7=8
  • forbids c7=8

Now we can solve some more cells again:

• c9 = 8% box & column
• c1 = 9% column
• i1 = 8% cell
• i7 = 9% cell
• d3 = 8% row & box
• g3 = 9% row & box

Possibility Matrix at UP 38

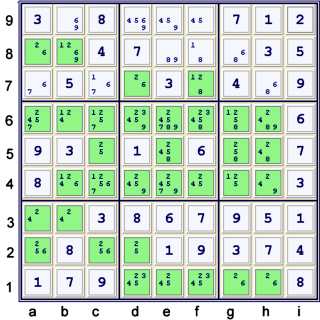
From this point, the puzzle solves quickly. One way to finish:

• Locked 2's at ab3
  • forbids ac2=2

Then:

• d2 = 2% row
• d7 = 6% cell
• % cells to the end

Solved Sudoku

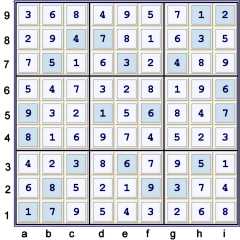
Proof

Here is the proof, pared down to required steps and presented in my usual style:

1. Start at 22 filled - the given puzzle. Unique Possibilities to 26 filled. (UP 26).
2. 1. Hidden pair 17 at e2f3 forbids e2=245, f3=248
   2. c9=8 == c7=8 -- c7=1 == f7=1 -- f3=1 == f3=7 -- g3=7 == g9=7 forbids g9=8,c9=7 UP 32
3. 1. fc on 8's:d3 == g3 -- g8 == ef8 forbids d79=8
   2. g8=6 == ab8=6 -- b9=6 == b9=9 -- b3=9 == g3=9 forbids g8=9
   3. Locked 9's at hi7 forbids cd7=9
   4. a8=2 == a8=6 -- g8=6 == i7=6 -- d7=6 == d7=2 forbids ac7,ef8=2
   5. c7=1 == f7=1 -- f8=1 == f8=8 -- g8=8 == hi7=8 forbids c7=8 UP 38
4. Locked 2's at ab3 forbids ac2=2 UP 81

• Sets: 2 + 4 + 2 + 3 + 1 + 3 + 3 + 1 = 19
• Max depth 4 at step 2.2
• Rating: 2(.01) + 2(.03) + 3(.07) + .15 = .37

Like most puzzles, there are many ways to tackle this one. Below find two alternate approaches.

Alternate Proof 1

Step 3.2 of this proof uses a forbidding chain element explained in Advanced Forbidding Chains.

1. Start at 22 filled - the given puzzle. Unique Possibilities to 26 filled. (UP 26).
2. 1. Hidden pair 17 at e2f3 forbids e2=245, f3=248
   2. c9=8 == c7=8 -- c7=1 == f7=1 -- f3=1 == f3=7 -- g3=7 == g9=7 forbids g9=8,c9=7 UP 32
3. 1. Locked 6's at ac2 forbids c1=6
   2. b9=9 == b9=6 -- a78=6 == a2=6 -- c2=6 =={pair 25 at c25} -- c1=25 == c1=9 forbids b3,c79=9 UP37
4. Locked 2's at ab3 forbids ac2=2 UP 81

• Sets: 2 + 4 + 1 + 5 + 1 = 13
• Max depth 5 at step 3.2
• Rating: 2(.01) + .03 + .15 + .31 = .51

Alternate Proof 2

Step 3.2 of this proof also uses a forbidding chain as a Boolean variable

1. Start at 22 filled - the given puzzle. Unique Possibilities to 26 filled. (UP 26).
2. 1. Hidden pair 17 at e2f3 forbids e2=245, f3=248
   2. c9=8 == c7=8 -- c7=1 == f7=1 -- f3=1 == f3=7 -- g3=7 == g9=7 forbids g9=8,c9=7 UP 32
3. 1. c5=2 == c5=5 -- a6=5 == a2=5 -- d2=5 == d2=2 forbids c2=2
      • Very common Y wing style above
   2. {pair 24 at ab3} == b3=9 -- b9=9 == b9=6 -- a8=6 == a8=2 forbids a2=2 UP 33
4. Triple 689 at dhi7 (dh7=689,i7=89) forbids ac7=6, af7=8, c7=9 UP 81

• Sets: 2 + 4 + 3 + 4 + 3 = 16
• Max depth 4 at steps 2.2 and 3.2
• Rating: .03 + 2(.07) + 2(.15) = .47

Proof choices

For every tough sudoku puzzle, there are many manners to come to the solution, and therefor many possible proofs. The choice as to which proof is better is a completely arbitrary one. I prefer proofs of less maximum depth, but as is illustrated above, adding a little bit of depth may reduce both the total strong sets considered and the total steps used in a proof. The ratings that I assign are my clumsy attempt at comparing proof complexity.

The choice of rating system is also completely arbitrary. For this reason, I like to provide the entire vector: Total sets, Maximum depth, rating. Of course, more factors could be considered. I am always hoping for someone to suggest a better, yet not overly complicated, way to evaluate puzzle proofs.