The following illustrated proof for the almost diabolical & extreme
Unsolvable #16 employs
an interesting variety of techniques. If this is
your first visit to this blog, WELCOME!!
I must apologize, as the terminology used here is not the standard terminolgy used in most other Sudoku
sites. Therefor, previous blog pages may be helpful. Links to these pages are found to the right,
under Sudoku Techniques. Specifically, one may want
to refer to the following pages:
The illustrations of forbidding chains, also called
Alternating Inference Chains (AIC), shown in this proof will share this key:
- black line = strong inference performed upon a set (strong link)
- red line = weak inference performed upon a set (weak link)
- black containers define a partioning of a strong set(s)
- candidates crossed out in red = candidates proven false
Please be aware that, for me,
strong and weak need not be mutually exclusive properties.
This puzzle is meant to be very difficult, but it is much easier than the previous unsolvable.
Unsolvable #16
Two Unique Possibilities are available here:
- c3 = 9% column & box (hidden single)
- i5 = 6% column & box
I like to look beyond the possibility matrix to find hidden sets at this time.
Hidden Pair 78, Hidden Triple 678, Locked candidate 4
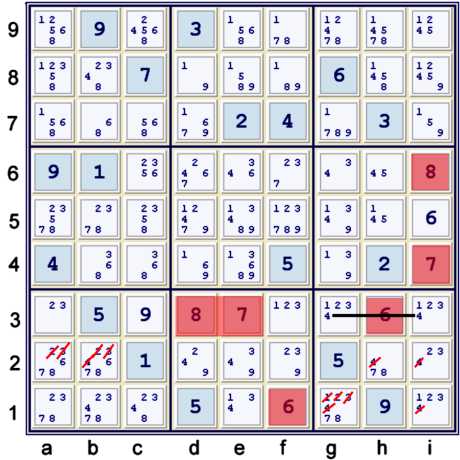
To save some space, I have chosen to illustrate a few steps simultaneously. The givens that are
highlit above help one locate the hidden sets illustrated. Also, I have illustrated the
Locked 4s eliminations. There are more locked sets eliminations available. This proof does
not require them, so I have not bothered to detatil those.
Almost Hidden Pair 23
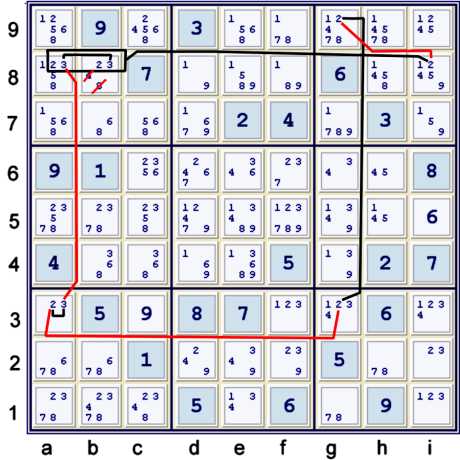
The graph above attempts to illustrate the following chain:
- b8=3 == a8=3 -- a3=3 == a3=2 -- g3=2 == g9=2 -- i8=2 == {Hidden Pair 23 at ab8}
Using the same strong inference sets, one can find a chain that also eliminates a15=3. Let me know
if you find it! It is often instructive to see how the same strong inferences can yield two
differing sets of eliminations. Usually some/most are common to both chains. In this case, the
chain I choose to not illustrate is the stronger one. You may also find a Sue De Cox above.
However, after solving c9=b1=4% column, a very short chain gets you to the same point.
My favorite Y wing style - also a Hub, Spoke Rim
Although b8=a3=23 is generally a marker for a Very Common Y Wing Style, in this case a
different Y wing Style exists. Illustrated above is a continuous loop, written as:
- a3=2 == a3=3 -- a8=3 == b8=3 -- b8=2 == a89=2 This proves:
- a3=3 == a8=3 => a15≠3
- a3=2 == a89=2 => a15≠2
- b8=3 == b8=2 , but we already had that
Usually, the continuous loop Y Wing Style will use at least one grouped argument. This
one uses a89=2. Also, this type of elimination and Sue De Cox tend to hang out together.
After making these eliminations, a naked pair 78 is revealed in row 1 => c1≠8
Hinged coloring with candidate 8
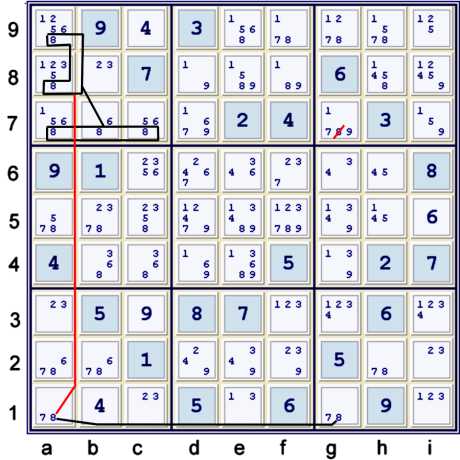
It is a common trick to use a candidate that is limited to one each of a row and a column within
a box. Above, this forbidding chain (AIC) on 8s is shown:
- abc7 == a89 -- a1 == g1 => g7≠8
This same pattern could also be written:
The key is the 8s must be in at least one of {row 7, column a}. Note here that it matters not even
if 8 were in both row 7 and column a.
A continuous loop considering 6 strong inferences
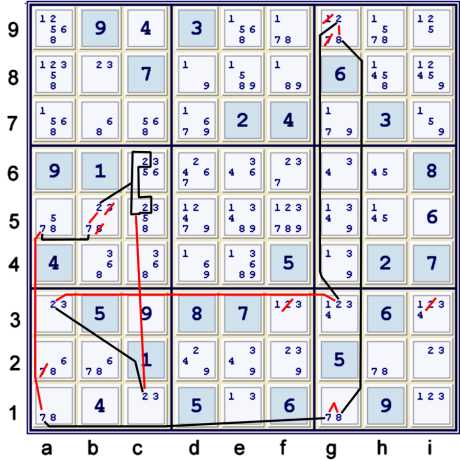
Illustrated above is another continuous loop, or wrap around, chain. One way of many to write it is:
- a1=7 == g1=7 -- g1=8 == g9=8 -- g9=2 == g3=2 -- a3=2 == c1=2 -- c56=2 == b5=2 -- b5=7 == a5=7 =>
- g1=7 == g1=8, but we have that already
- g9=8 == g9=2 => g9=28
- g3=2 == a3=2 => fi3≠2
- c1=2 == c56=2, but we also have that previously
- b5=2 == b5=7 => b5=27
- a1=7 == a5=7 => a2≠7
Continuous loops have been treated in some previous blog pages. If the reasons for all of the eliminations
are not clear, perhaps review some of those pages.
A supefluous Y Wing Style
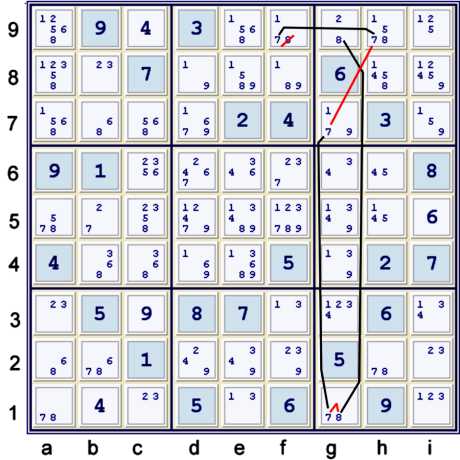
There are many Y wing styles available in this puzzle. I decided to illustrate this one primarily
because it makes the following step easier. Just for fun, try to do the following step without
executing this step. Hint: it is very similar, but is an Advanced Forbidding Chain.
The step above as a forbidding chain (AIC):
- f9=7 == h9=7 -- g7=7 == g1=7 -- g1=8 == g9=8 => f9≠8
A standard loop considering 6 strong inferences
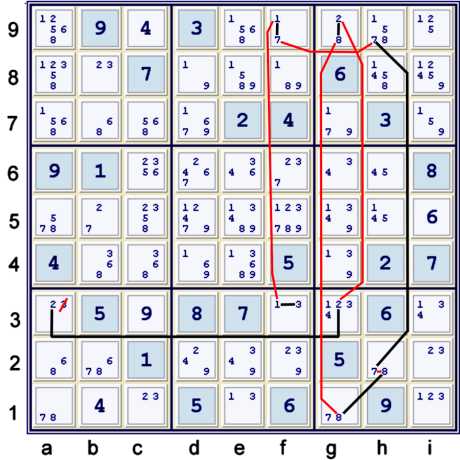
Illustrated above is the following chain:
- a3=2 == g3=2 -- g9=2 == g9=8 -- g1=8 == h2=8 -- h2=7 == h9=7 -- f9=7 == f9=1 -- f3=1 == f3=3
After making the indicated elimination, the puzzle cascades with
Unique Possibilities (both
naked and hidden singles) until 50 cells are solved. (UP 50).
Very Common Y Wing Style
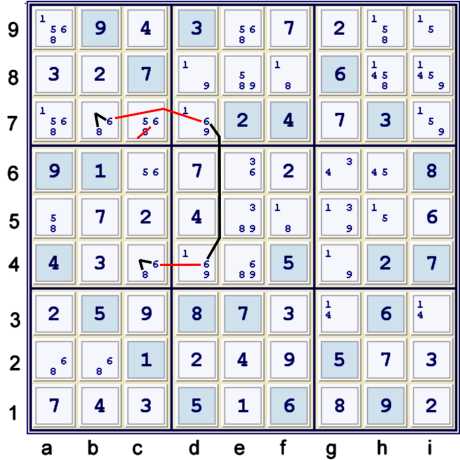
There are many easy ways to finish this puzzle from this point. The most efficient way that
I found to complete the puzzle with just one easy elimination is illustrated above:
- c4=8 == c4=6 -- d4=6 == d7=6 -- b7=6 == b7=8 => c7≠8
Again, it may bear repeating that this type of Y Wing Style should be considered standard issue.
The puzzle is reduced to naked singles to the end.
Solution
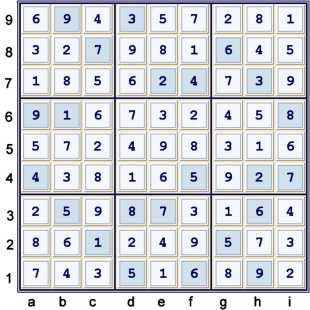
PROOF
- Start with the given puzzle. Unique Possibilities to 25 filled. (UP 25)
- Hp 78 at g1h2 => g1h2=78
- Ht 678 at abh2 => ab2=678
- Locked 4s at gi3 =>i12≠4
- alternate
b8=2 == {fc on 2s:a8 == i8 -- g9 == g3} -- a3=2 == a3=3-- a8=3 == b8=3
UP 27- Y style: a3=2 == a3=3 -- a8=3==b8=3 -- b8=2 ==a89 =2 => a15≠2
- pair 78 at ag1 => c1≠8/li>
- fc on 8's: bc7 == a789 -- a1 == g1 => g7≠8/li>
- g3=2 == g9=2 -- g9=8 == g1=8 -- g1=7 == a1=7 -- a5=7 == b5=7 -- b5=2
== b8=2 == a89=2 == a3=2
- => if3≠2, g9≠17, a2≠7, b5≠38
- a3=2 == a3=3 -- f3=3 == f3=1 -- f9=1 == {VCY style f9=8 == f9=7 -- h9=7
== h2=7 -- g1=7 == g1=8} -- g9=8 == g9=2
UP 50- vcystyle: c4=8 == c4=6 -- d4=6 == d7=6 -- b7=6 == b7=8 => c7≠8 UP 81
- Sets: 2 + 3 + 1 + 4 + 3 + 2 + 2 + 6 + 6 + 3 = 32
- Rating: .01 + 3(.03) + 3(.07) + .15 + 2(.63) = 1.72
- Max depth 6 at steps 3d,3e.
NOTES
This puzzle does not quite deserve the label, unsolvable. I am fairly certain that the path
that I illustrated is not the most efficient path. Unlike unsolvable 13, there was never a point
in this puzzle that I had to look for chains. Therefor, I did not take much time to optimize my
proof. However, this is an excellent puzzle for study, as it has some nice and heavily indicated
chains to find. Hopefully, many of you are able to chain straight through!